ข้อสอบคัดเลือกของทีม USA 2009 (25 ข้อ)
| 1. | แอปเปิ้ลขนาด 0.3 kg เดิมอยู่นิ่ง ร่วงลงมาจากความสูง 40 cm ลงบนพื้นราบ และหยุดนิ่งใน 0.1 s พื้นผิวที่ตกกระแทกพื้นเท่ากับ 4 cm2 แล้วความดันเฉลี่ยของแอปเปิ้ลขณะตกกระแทกพื้นเท่ากับข้อใด ไม่ต้องคำนึงถึงแรงต้านอากาศ |
| A | 67,000 Pa |
| B | 21,000 Pa |
| C | 6,700 Pa |
| D | 210 Pa |
| E | 67 Pa |
ตอบ (B)
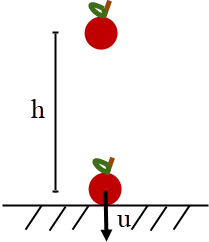จาก v ที่แอปเปิ้ลตกพื้น \({\rm{ = }}\sqrt {{\rm{2gh}}}\) จะได้
โมเมนตัม \(\rm = m\sqrt {2gh}\)
เมื่อกระทบพื้นโมเมนตัมจะถูกเปลี่ยนเป็นแรงดล จะได้
\(\begin{align*}
{\rm{m}}\sqrt {{\rm{2gh}}} &= \rm F\Delta t\\
{\rm{m}}\sqrt {{\rm{2gh}}} &= \rm PA\Delta t\\
\rm P &= \frac{{{\rm{m}}\sqrt {{\rm{2gh}}} {\rm{ }}}}{{{\rm{A\Delta t}}}}\\
\rm P &= \frac{{{\rm{(0}}{\rm{.3)}}\sqrt {{\rm{2}} \times {\rm{10}} \times {\rm{0}}{\rm{.4}}} {\rm{ }}}}{{{\rm{4}} \times {\rm{1}}{{\rm{0}}^{{\rm{ - 4}}}} \times 0.1}}\\
\rm P &= \frac{{0.8485{\rm{ }}}}{{0.4}} \times {\rm{1}}{{\rm{0}}^{{\rm{ - 4}}}}\\
\rm P &= 2.121 \times {\rm{1}}{{\rm{0}}^{{\rm{ - 4}}}}\,\,\,{\rm{N/}}{{\rm{m}}^{\rm{2}}}\\
{\rm{P}} &\approx 21,000\,\,{\rm{Pa}}
\end{align*}\)
| 2. | วัตถุที่เหมือนกัน 3 ชิ้น ถูกวางโต๊ะที่ไม่มีแรงเสียดทาน ดังรูป ให้มวลที่อยู่ตรงกลางอยู่นิ่ง ส่วนอีกสองชิ้นพุ่งเข้าหาวัตถุที่อยู่ตรงกลางด้วยอัตราเร็ว v เหมือนกัน โดยวัตถุที่อยู่ตรงกลางจะอยู่ใกล้กับวัตถุทางซ้ายมากกว่าทางขวา และการเคลื่อนที่ทั้งหมดเกิดขึ้นหนึ่งมิติ ตามแนวนอน
 |
| A | วัตถุตรงกลาง จะเคลื่อนที่ไปทางซ้าย |
| B | วัตถุตรงกลาง จะเคลื่อนที่ไปทางขวา |
| C | วัตถุตรงกลาง หยุดนิ่งอยู่ทางด้านซ้ายของตำแหน่งเริ่มต้น |
| D | วัตถุตรงกลาง หยุดนิ่งอยู่ที่ตำแหน่งเริ่มต้น |
| E | วัตถุตรงกลาง หยุดนิ่งอยู่ทางด้านขวาของตำแหน่งเริ่มต้น |
ตอบ (D)
แบ่งเป็น 3 เหตุการณ์ย่อยๆ
1. วัตถุทางซ้าย ชน วัตถุตรงกลาง
อนุรักษ์ \({\rm{\vec P}}\)
2. วัตถุทางขวา ชน วัตถุตรงกลาง
อนุรักษ์ \({\rm{\vec P}}\)
ดังนั้น วัตถุตรงกลางจะสะท้อนกลับ แล้ววิ่งไปทางซ้ายด้วยความเร็ว v
วัตถุทางขวาจะสะท้อนกลับ แล้ววิ่งไปทางขวาด้วยความเร็ว v
3. วัตถุตรงกลาง ชน วัตถุทางซ้าย ซึ่งหยุดนิ่งอยู่ ณ ตำแหน่งเริ่มต้นของวัตถุกลาง
ในทำนองเดียวกับเหตุการณ์ในข้อ 1 หลังชนวัตถุทางซ้ายจะเคลื่อนที่ไปทางซ้ายด้วยอัตราเร็ว v และวัตถุตรงกลางจะหยุดนิ่ง ณ ตำแหน่งเริ่มต้นของมัน
ดังนั้น ตอบข้อ (D)
แบ่งเป็น 3 เหตุการณ์ย่อยๆ
1. วัตถุทางซ้าย ชน วัตถุตรงกลาง
\({\rm{mv = mv' + mu }} \Rightarrow {\rm{ v' = v }} - {\rm{ u}}\)
อนุรักษ์ E
\(\begin{align*} \frac{{\rm{1}}}{{\rm{2}}}{\rm{m}}{{\rm{v}}^{\rm{2}}} &= \frac{{\rm{1}}}{{\rm{2}}}{\rm{m(}}{{{\rm{v'}}}^{\rm{2}}} + {u^2})\\ {v^2} &= {(v - u)^2} + {u^2}\\ 2{\rm{uv}} &= {u^2}\\ {\rm{u}} &= 0,\rm\not{2}\not v\\ {\rm{v}} &= \rm v,\rm\not -\not v \end{align*}\)
ดังนั้น วัตถุตรงกลางเคลื่อนที่ไปทางขวา ด้วยความเร็ว v ส่วนวัตถุทางซ้ายหยุดนิ่งอยู่ ณ ตำแหน่งเริ่มต้นของวัตถุกลาง2. วัตถุทางขวา ชน วัตถุตรงกลาง
\({\rm{0 = m}}{{\rm{v}}_1}{\rm{ + m}}{{\rm{v}}_2}{\rm{ }} \Rightarrow {\rm{ }}{{\rm{v}}_1}{\rm{ = }} - {\rm{ }}{{\rm{v}}_{\rm{2}}}\)
อนุรักษ์ E
\(\begin{align*} \frac{{\rm{1}}}{{\rm{2}}}{\rm{m (}}{{\rm{v}}^{\rm{2}}} + {{\rm{v}}^{\rm{2}}}) &= \frac{{\rm{1}}}{{\rm{2}}}{\rm{m(}}{{\rm{v}}_1}^{\rm{2}} + {{\rm{v}}_2}^{\rm{2}})\\ 2{v^2} &= 2{{\rm{v}}_1}^2\\ {{\rm{v}}_1} &= \rm\not v, - v\\ {{\rm{v}}_2} &= \rm\not- \not v ,v \end{align*}\)
ค่าที่ตัดออก คือ ค่าที่สื่อว่าวัตถุทะลุผ่านกันไป ซึ่งเป็นไปไม่ได้ดังนั้น วัตถุตรงกลางจะสะท้อนกลับ แล้ววิ่งไปทางซ้ายด้วยความเร็ว v
วัตถุทางขวาจะสะท้อนกลับ แล้ววิ่งไปทางขวาด้วยความเร็ว v
3. วัตถุตรงกลาง ชน วัตถุทางซ้าย ซึ่งหยุดนิ่งอยู่ ณ ตำแหน่งเริ่มต้นของวัตถุกลาง
ในทำนองเดียวกับเหตุการณ์ในข้อ 1 หลังชนวัตถุทางซ้ายจะเคลื่อนที่ไปทางซ้ายด้วยอัตราเร็ว v และวัตถุตรงกลางจะหยุดนิ่ง ณ ตำแหน่งเริ่มต้นของมัน
ดังนั้น ตอบข้อ (D)
| 3. | วัตถุที่เหมือนกัน 3 ชิ้น ถูกวางโต๊ะที่ไม่มีแรงเสียดทาน ดังรูป ให้มวลที่อยู่ตรงกลางอยู่นิ่ง ส่วนอีกสองชิ้นพุ่งเข้าหาวัตถุที่อยู่ตรงกลางด้วยอัตราเร็ว v เหมือนกัน โดยวัตถุที่อยู่ตรงกลางจะอยู่ใกล้กับวัตถุทางซ้ายมากกว่าทางขวา และการเคลื่อนที่ทั้งหมดเกิดขึ้นหนึ่งมิติ ตามแนวนอน
 |
| A | วัตถุตรงกลาง จะเคลื่อนที่ไปทางซ้าย |
| B | วัตถุตรงกลาง จะเคลื่อนที่ไปทางขวา |
| C | วัตถุตรงกลาง หยุดนิ่งอยู่ทางด้านซ้ายของตำแหน่งเริ่มต้น |
| D | วัตถุตรงกลาง หยุดนิ่งอยู่ที่ตำแหน่งเริ่มต้น |
| E | วัตถุตรงกลาง หยุดนิ่งอยู่ทางด้านขวาของตำแหน่งเริ่มต้น |
ตอบ (E)
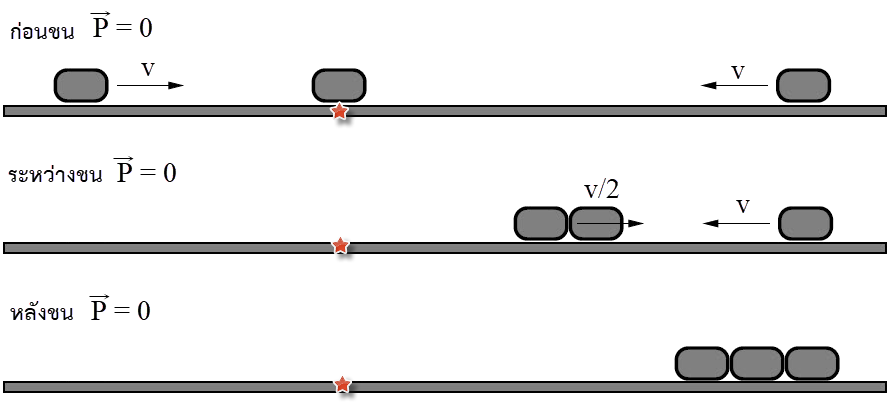สุดท้ายวัตถุทั้งสามจะหยุดนิ่ง เพราะ
1. \(\overrightarrow {\rm{P}} = 0\) จากกฏอนุรักษ์โมเมนตัม
2. มวล 3 ก้อนติดกันเป็นก้อนเดียว
ดังนั้น ความเร็วของมวลทั้งสามเป็น 0 และหยุดนิ่งอยู่ทางด้านขวาของตำแหน่งเริ่มต้น
1. \(\overrightarrow {\rm{P}} = 0\) จากกฏอนุรักษ์โมเมนตัม
2. มวล 3 ก้อนติดกันเป็นก้อนเดียว
ดังนั้น ความเร็วของมวลทั้งสามเป็น 0 และหยุดนิ่งอยู่ทางด้านขวาของตำแหน่งเริ่มต้น
| 4. | นักบินอวกาศมวล 80 kg นั่งอยู่บนยานอวกาศที่กำลังเข้าใกล้พื้นโลก ถ้ายานอวกาศมีความเร่งในทิศขึ้นตั้งฉากกับพื้นโลกเป็นห้าเท่าของความเร่งโน้มถ่วง แล้วแรงที่นักบินกระทำกับยานอวกาศจะเท่ากับข้อใด |
| A | 4800 N |
| B | 4000 N |
| C | 3200 N |
| D | 800 N |
| E | 400 N |
ตอบ (A)
ให้ N เป็นแรงที่ยานทำกับนักบินอวกาศ
กฏของนิวตัน
ดังนั้น แรงที่นักบินกระทำกับยานอวกาศเท่ากับ 4800 N
ให้ N เป็นแรงที่ยานทำกับนักบินอวกาศ
กฏของนิวตัน
\(\begin{align*}
{\rm{N}} - {\rm{mg}} &= {\rm{m(5g)}}\\
{\rm{N}} &= {\rm{mg = 6 \times 80 \times 10 = 4,800 N}}
\end{align*}\)
จากกฏข้อที่ 3 ของนิวตัน (action = reaction) จะได้ว่า แรงที่นักบินอวกาศทำกับยาน เท่ากับ แรงที่ยานทำกับนักบินอวกาศดังนั้น แรงที่นักบินกระทำกับยานอวกาศเท่ากับ 4800 N
| 5. | ดาวเทียมขนาดเท่ากันสามดวง A, B และ C อยู่ในวงโคจรของดาวเคราะห์ ตามรูป ถ้าขนาดของโมเมนตัมเชิงมุมของดาวเทียมที่วัดจากดาวเคราะห์ เท่ากับ LA , LB และ LC แล้วข้อใดต่อไปนี้ถูกต้อง
 |
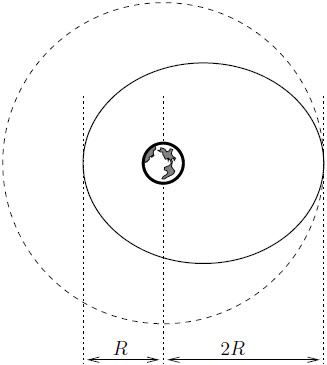| A | LA > LB > LC |
| B | LC > LB > LA |
| C | LB > LC > LA |
| D | LB > LA > LC |
| E | การจัดลำดับขนาดจะแตกต่างกัน ขึ้นอยู่กับช่วงเวลานั้นๆ |
ตอบ (A)
เปรียบเทียบ A, C
จาก vA > vC และ rA > rC ดังนั้น LA > LB
เปรียบเทียบ B, C
พิจารณาจุด B ตรงไหนก็ได้ เพราะ \({\overrightarrow {\rm{L}} _{\rm{B}}}\) รอบโลกคงที่ เนื่องจากไม่มีทอร์กภายนอกมากระทำ
ดังนั้น เมื่อย้าย B มาที่ rB = rC จะได้ vB > vC เพราะ การโคจรเป็นวงรี ต้องใช้พลังงานมากกว่าการโคจรเป็นวงกลม ดังนั้น LB > LC
สรุปว่า LA > LB > LC
เปรียบเทียบ A, C
จาก vA > vC และ rA > rC ดังนั้น LA > LB
เปรียบเทียบ B, C
พิจารณาจุด B ตรงไหนก็ได้ เพราะ \({\overrightarrow {\rm{L}} _{\rm{B}}}\) รอบโลกคงที่ เนื่องจากไม่มีทอร์กภายนอกมากระทำ
ดังนั้น เมื่อย้าย B มาที่ rB = rC จะได้ vB > vC เพราะ การโคจรเป็นวงรี ต้องใช้พลังงานมากกว่าการโคจรเป็นวงกลม ดังนั้น LB > LC
สรุปว่า LA > LB > LC
| 6. | วัตถุถูกโยนด้วยอัตราเร็วต้นคงที่ v0 ด้วยมุมที่แตกต่างกัน α กับแนวราบ ที่ความสูงคงที่ค่าหนึ่ง h เหนือจุดยิง อัตราเร็ว v ของวัตถุจะมีค่าตามฟังก์ชันของมุมเริ่มต้น α ข้อใดอธิบาย v ที่เปลี่ยนไปตามมุม α ได้ดีที่สุด (สมมุติว่า มีความสูง h ตามเงื่อนไข และไม่มีแรงต้านอากาศ) |
| A | v จะเพิ่มขึ้นเป็นลำดับทางเดียวตาม α |
| B | v จะเพิ่มขึ้นถึงค่าวิกฤต vmax ค่าหนึ่ง หลังจากนั้นจะลดลง |
| C | v จะคงที่ โดยไม่ขึ้นกับ α |
| D | v จะลดลงถึงค่าวิกฤต vmin ค่าหนึ่ง หลังจากนั้นจะเพิ่มขึ้น |
| E | ไม่มีข้อใดถูก |
ตอบ (C)
จากกฏการอนุรักษณ์พลังงาน
จากกฏการอนุรักษณ์พลังงาน
\(\begin{align*} \frac{{\rm{1}}}{{\rm{2}}}{\rm{m}}{{\rm{v}}_{\rm{0}}}^{\rm{2}}{\rm{ = }}\frac{{\rm{1}}}{{\rm{2}}}{\rm{m}}{{\rm{v}}^{\rm{2}}}{\rm{ + mgh}}\\ {\rm{v = }}\sqrt {{{\rm{v}}_{\rm{0}}}^{\rm{2}} - 2{\rm{gh}}} \end{align*}\)
สังเกตว่า v ไม่ได้ขึ้นกับ α| 7. | นกตัวหนึ่งบินเป็นเส้นตรง โดยตอนแรกบิน 10 m/s แล้วเพิ่มอัตราเร็วอย่างสม่ำเสมอจนถึง 15 m/s ได้ระยะทางทั้งหมด 25 m ความเร่งของนกเท่ากับข้อใด |
| A | 5.0 m / s2 |
| B | 2.5 m / s2 |
| C | 2.0 m / s2 |
| D | 0.5 m / s2 |
| E | 0.2 m / s2 |
ตอบ (B)
จาก \({\rm{a = }}\dfrac{{{\rm{dv}}}}{{{\rm{dt}}}}\) จะได้ว่า
จากโจทย์เขียนกราฟได้ ดังนี้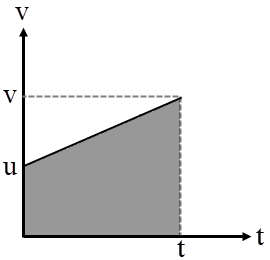
ให้ S เป็นพื้นที่ใต้กราฟ
จาก \({\rm{a = }}\dfrac{{{\rm{dv}}}}{{{\rm{dt}}}}\) จะได้ว่า
\(\begin{align*} \,\,\int\limits_{\rm{u}}^{\rm{v}} \rm dv &= {\int\limits_{\rm{0}}^{\rm{t}} {{\rm{adt}}} } \\ {\rm{v}} - {\rm{u}} &= {\rm{at}} \end{align*}\)
จะได้ว่า \({\rm{t}} = \dfrac{{{\rm{v}} - {\rm{u}}}}{{\rm{a}}}\) และ \({\rm{v}} = {\rm{u + at}}\)จากโจทย์เขียนกราฟได้ ดังนี้
\(\begin{align*} {\rm{S}} &= \frac{1}{2}\left( {{\rm{v + u}}} \right){\rm{t}}\\ \rm{S} &= \frac{1}{2}\left( {{\rm{v + u}}} \right)\left( {\frac{{{\rm{v}} - {\rm{u}}}}{{\rm{a}}}} \right)\\ {\rm{a}} &= \frac{{{{\rm{v}}^2} - {{\rm{u}}^2}}}{{2{\rm{S}}}} = \frac{{{\rm{1}}{{\rm{5}}^2} - {\rm{1}}{{\rm{0}}^2}}}{{2{\rm{(25)}}}} = 2.5\,\,{\rm{m / }}{{\rm{s}}^{\rm{2}}} \end{align*}\)
| 8. | ให้แผ่นกลมหมุนรอบแกนที่ผ่านจุดศูนย์กลาง และตั้งฉากกับระนาบของแผ่นกลม ด้วยความเร็วเชิงมุมตามกราฟด้านล่าง
 |
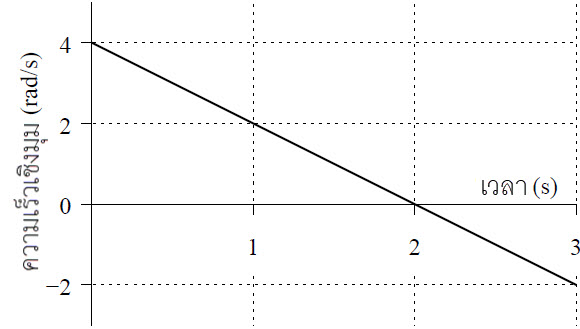| A | – 12 rad / s2 |
| B | – 8 rad / s2 |
| C | – 4 rad / s2 |
| D | – 2 rad / s2 |
| E | 0 rad / s2 |
ตอบ (B)
ให้ α = ความเร่งเชิงมุม (rad/s2) และ ω = ความเร็วเชิงมุม (rad/s)
ให้ α = ความเร่งเชิงมุม (rad/s2) และ ω = ความเร็วเชิงมุม (rad/s)
\({\rm{\alpha = }}\dfrac{{{\rm{\Delta \omega }}}}{{{\rm{\Delta t}}}} = \dfrac{{0 - 4}}{{2 - 0}} = - 2\,\,\,{\rm{rad/}}{{\rm{s}}^2}\)
| 9. | ให้แผ่นกลมหมุนรอบแกนที่ผ่านจุดศูนย์กลาง และตั้งฉากกับระนาบของแผ่นกลม ด้วยความเร็วเชิงมุมตามกราฟด้านล่าง
 |
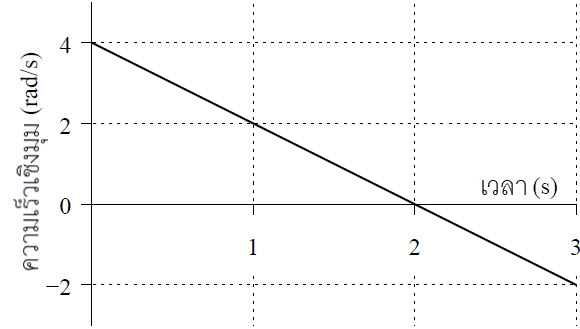| A | 9 rad |
| B | 8 rad |
| C | 6 rad |
| D | 4 rad |
| E | 3 rad |
ตอบ (E)
ให้ θ = มุมที่กวาดไป (rad)
จาก θ เป็นพื้นที่ใต้กราฟ ω – t จะได้ว่า
ให้ θ = มุมที่กวาดไป (rad)
จาก θ เป็นพื้นที่ใต้กราฟ ω – t จะได้ว่า
\({\rm{\theta }} = \dfrac{1}{2}(4)(2) - \dfrac{1}{2}(2)(1) = \,\,\,3\,\,\rm rad\)
| 10. | ชายคนหนึ่งยืนอยู่ที่ขอบประตูหนีไฟ เขาขว้างแอปเปิ้ลสองลูกพร้อมกัน โดยอันหนึ่งโยนขึ้นด้วยอัตราเร็ว 7 m/s และอีกอันขว้างลงด้วยอัตราเร็วเท่ากัน ระยะห่างของแอปเปิ้ลทั้งสองที่ วินาทีที่ 2 หลังโยนออกไปเท่ากับข้อใด สมมุติว่าทั้งสองยังไม่ตกถึงพื้น |
| A | 14 m |
| B | 20 m |
| C | 28 m |
| D | 34 m |
| E | 56 m |
ตอบ (C)
เมื่อเวลาผ่านไป 2 วินาที
\(\begin{align*} {{\rm{s}}_1} &= 7(2) - \frac{1}{2}(10)({2^2})\\ \rm s_2 &= 7(2) + \frac{1}{2}(10)({2^2})\\ {{\rm{s}}_1} + {{\rm{s}}_{\rm{2}}} &= 7(2) + 7(2) = \rm 28~m \end{align*}\)
| 11. | มวล 2.25 kg มีการเร่งอัตราเร็วดังกราฟ งานที่กระทำกับมวลได้เท่ากับข้อใด |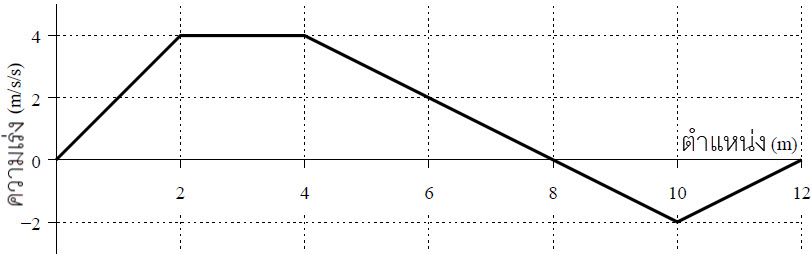
| A | 36 J |
| B | 22 J |
| C | 5 J |
| D | – 17 J |
| E | – 36 J |
ตอบ (A)
\(\begin{align*} \rm{W} &= \int {\overrightarrow {\rm{F}} \cdot {\rm{d}}} \overrightarrow {\rm{s}} \\ &= {\rm{m}}\int {\overrightarrow {\rm{a}} \cdot {\rm{d}}\overrightarrow {\rm{s}} } \\ &= \rm m\left( {\frac{1}{2}(4)(8 + 2) - \frac{1}{2}(4)(2)} \right)\\ &=\frac{9}{4}\left( {20 - 4} \right)\\ &= 36\,\,{\rm{J}} \end{align*}\)
| 12. | แบทแมนมวล M = 100 kg ปีนขึ้นดาดฟ้าสูง 30 m จากนั้นโยนเชือกเบาให้โรบินจับไว้ แล้วดึงโรบินที่มีมวลประมาณ 75 kg ขึ้นมาบนดาดฟ้า งานสุทธิที่แบทแมนทำหลังโรบินขึ้นมาบนดาดฟ้าได้เท่ากับข้อใด |
| A | 60 J |
| B | 7 × 103 J |
| C | 5 × 104 J |
| D | 600 J |
| E | 3 × 104 J |
ตอบ (C)
\(\begin{align*}
{\rm{W}} &= {{\rm{M}}_{{\rm{total}}}}{\rm{gh}}\\
&= (100 + 75) \times 10 \times 30\\
&= 525 \times {10^2}\\
&\approx 5 \times {10^4}\,\,{\rm{J}}
\end{align*}\)
| 13. | ก (มวล 33.1 kg) ข (มวล 63.7 kg) และ ค (มวล 24.3 kg) นั่งห่างกันบนกระดานหกสม่ำเสมอที่มีน้ำหนักเบา เว้นระยะห่าง 2.74 m ตามลำดับ (ข อยู่ระหว่าง ก และ ค) ทำให้กระดานหกสมดุล ใครมีทอร์กบนกระดานหกมากที่สุด (ในแง่ของขนาด) ไม่ต้องสนมวลของกระดานหก |
| A | ก |
| B | ข |
| C | ค |
| D | ทั้งสามมีทอร์กเท่ากัน |
| E | ข้อมูลไม่เพียงพอต่อการตอบคำถาม |
ตอบ (B)
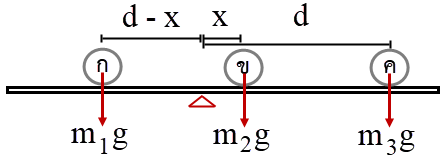กระดานหกสมดุลแสดงว่า ทอร์กรวมรอบจุดหมุนเท่ากับ 0
\(\begin{align*} \rm{{\rm{m}}_{\rm{1}}}{\rm{g}}(d - x) &= \rm{m_2}gx + {m_3}g(d + x)\\ \rm\frac{{{\rm{d}}({m_1} - {m_3})}}{{{m_1} + {m_2} + {m_3}}} &= {\rm{x}} \end{align*}\)
ทอร์กของ ก
\(\begin{align*} \rm{{\rm{m}}_{\rm{1}}}{\rm{g}}(d - x) &= \rm{m_1}g\left( {\frac{{({m_2} + 2{m_3})}}{{{m_1} + {m_2} + {m_3}}}} \right)d\\ &\propto \rm {m_1}({m_2} + 2{m_3}) \approx 30(110) \approx 3300 \end{align*}\)
ทอร์กของ ข
\(\rm{{\rm{m}}_2}{\rm{g}}x \propto {m_2}({m_1} - {m_3}) \approx 60(10) \approx 600\)
ทอร์กของ ค
\(\rm{{\rm{m}}_3}{\rm{g(d + }}x) \propto {m_3}(2{m_1} + {m_2}) \approx 20(60 + 60) \approx 2400\)
ดังนั้น ก มีทอร์กบนกระดานหกมากที่สุด| 14. | บล็อคไม้ (มวล M) ถูกแขวนบนเชือกเบาที่ถูกปักหมุดไว้ กระสุนที่มาด้วยอัตราเร็ว (มีมวล m และอัตราเร็วต้น v0) ชนกับบล็อคที่เวลา t = 0 และฝังอยู่ในนั้น ถ้า S เป็นระบบที่ประกอบด้วย บล็อกและกระสุน แล้วปริมาณใดที่ถูกอนุรักษ์ไว้ในช่วง t = –10 s ถึง t = +10 s
 |
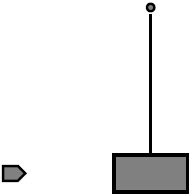| A | โมเมนตัมเชิงเส้นรวมของ S |
| B | องค์ประกอบในแนวนอนของ โมเมนตัมเชิงเส้นของ S |
| C | พลังงานกลของ S |
| D | โมเมนตัมเชิงมุมของ S ที่วัดเทียบกับแกนตั้งฉากกับหมุด |
| E | ไม่มีปริมาณใดถูกอนุรักษ์ไว้ |
ตอบ (E)
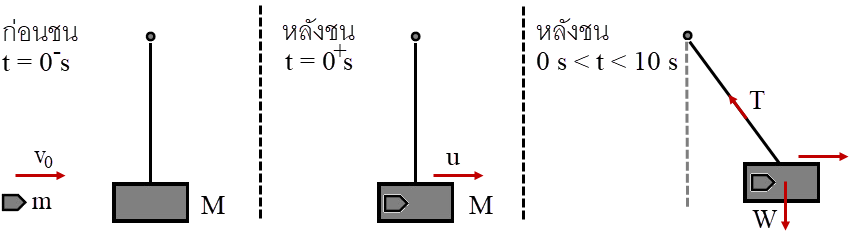พิจารณาแต่ละข้อ
(A) \(\overrightarrow {\rm{P}}\) ไม่อนุรักษ์ เพราะไม่มีแรงกระทำต่อระบบ ดังนั้น โมเมนตัมเชิงเส้นจะไม่ถูกอนุรักษ์ไว้
(B) Py ไม่อนุรักษ์ เพราะมีน้ำหนัก W และ Component แกน y ของ T กระทำต่อระบบ
(C) E ไม่อนุรักษ์ เพราะที่เวลา t = 0- s ถึง t = 0+ s มีการชนแบบไม่ยืดหยุ่น (กระสุนฝังติดไปกับบล็อคไม้)
(D) \(\overrightarrow {\rm{L}}\) ไม่อนุรักษ์ เพราะมี W กระทำต่อระบบซึ่ง W กระทำต่อแนวแรงไม่ผ่านจุดหมุน ทำให้เกิดทอร์กกระทำต่อระบบ
ดังนั้น ตอบ (E) ไม่มีข้อใดอนุรักษ์
(A) \(\overrightarrow {\rm{P}}\) ไม่อนุรักษ์ เพราะไม่มีแรงกระทำต่อระบบ ดังนั้น โมเมนตัมเชิงเส้นจะไม่ถูกอนุรักษ์ไว้
(B) Py ไม่อนุรักษ์ เพราะมีน้ำหนัก W และ Component แกน y ของ T กระทำต่อระบบ
(C) E ไม่อนุรักษ์ เพราะที่เวลา t = 0- s ถึง t = 0+ s มีการชนแบบไม่ยืดหยุ่น (กระสุนฝังติดไปกับบล็อคไม้)
(D) \(\overrightarrow {\rm{L}}\) ไม่อนุรักษ์ เพราะมี W กระทำต่อระบบซึ่ง W กระทำต่อแนวแรงไม่ผ่านจุดหมุน ทำให้เกิดทอร์กกระทำต่อระบบ
ดังนั้น ตอบ (E) ไม่มีข้อใดอนุรักษ์
| 15. | กระเป๋าเดินทาง 22.0 kg ถูกลากด้วยอัตราเร็วคงที่ 1.10 m/s เป็นเส้นตรง โดยนักเรียนคนหนึ่งที่จะไปสอบ IPhO ครั้งที่ 40 ที่ประเทศเม็กซิโก ถ้าเขาลากกระเป๋าที่สนามบินด้วยแรง 1.00×102 N เอียงทำมุมสูง 30.0 องศากับแนวระดับ แล้วสัมประสิทธิ์แรงเสียดทานจลน์ ระหว่างกระเป๋าเดินกับพื้นเท่ากับข้อใด |
| A | μk = 0.013 |
| B | μk = 0.394 |
| C | μk = 0.509 |
| D | μk = 0.866 |
| E | μk = 1.055 |
ตอบ (C)
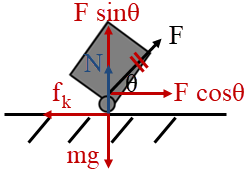กระเป๋าเคลื่อนที่ด้วยความเร็วคงที่ นั่นคือ \(\overrightarrow {\rm{a}} {\rm{ = 0}}\) ดังนั้น \(\sum {\overrightarrow {\rm{F}} } = 0\)
จาก \(\sum {{{\rm{F}}_{\rm{x}}}} = 0\) จะได้ว่า
จาก \(\sum {{{\rm{F}}_{\rm{x}}}} = 0\) จะได้ว่า
\(\begin{align*} {{\rm{f}}_{\rm{k}}}{\rm{ = Fcos\theta }}\\ {{\rm{\mu }}_{\rm{k}}}{\rm{N = Fcos\theta }} \end{align*}\)
จาก \(\sum {{{\rm{F}}_{\rm{y}}}} = 0\) จะได้ว่า
\(\begin{align*} \rm N + Fsin\theta &= \rm mg\\ \rm N &= \rm mg - {\rm{Fsin\theta }}\\ \end{align*}\)
แทน \(\rm N\) ใน \({{\rm{\mu }}_{\rm{k}}}{\rm{N = Fcos\theta }}\) จะได้
\(\begin{align*} {{\rm{\mu }}_{\rm{k}}}\left( {{\rm{mg}} - {\rm{Fsin\theta }}} \right) &= \rm Fcos\theta \\ {{\rm{\mu }}_{\rm{k}}} &= \frac{{{\rm{Fcos\theta }}}}{{{\rm{mg}} - {\rm{Fsin\theta }}}} \end{align*}\)
แทนค่า
\({{\rm{\mu }}_{\rm{k}}}{\rm{ = }}\dfrac{{{\rm{100}}\left( {\frac{{\sqrt 3 }}{2}} \right)}}{{{\rm{220}} - {\rm{100}}\left( {\frac{1}{2}} \right)}} = \dfrac{{5\sqrt 3 }}{{17}} \approx 0.509\)
| 16. | วัตถุมวล m สองอันที่เหมือนกัน นำไปติดที่ปลายทั้งสองของสปริง ที่มีค่านิจสปริง k และวางอยู่บนพื้นที่ไม่แรงเสียดทานในแนวนอน แล้วที่ความถี่เชิงมุม ω ขณะระบบสั่นเท่ากับข้อใด |
| A | \(\rm\sqrt{k/m}\) |
| B | \(\rm\sqrt{2k/m}\) |
| C | \(\rm\sqrt{k/2m}\) |
| D | \(2\rm\sqrt{k/m}\) |
| E | \(\rm\sqrt{k/m}/2\) |
ตอบ (B)
จากโจทย์ระบบจะสั่นรอบจุด cm ของระบบโดยที่ cm อยู่กับที่ เนื่องจากไม่มีแรงภายนอกมากระทำ
ดังนั้น มองว่าจุด cm เป็นกำแพง มีเพียง m 1 มวล และสปริงสั้นลงครึ่งหนึ่ง (k’ = 2k)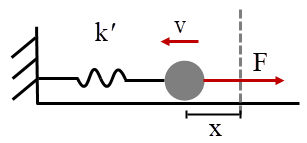
จากกฏของนิวตัน
จากโจทย์ระบบจะสั่นรอบจุด cm ของระบบโดยที่ cm อยู่กับที่ เนื่องจากไม่มีแรงภายนอกมากระทำ
ดังนั้น มองว่าจุด cm เป็นกำแพง มีเพียง m 1 มวล และสปริงสั้นลงครึ่งหนึ่ง (k’ = 2k)
\(\begin{align*} - \rm k'x &= \rm m\ddot x\\ \rm \ddot x &= - \frac{{{\rm{k'}}}}{{\rm{m}}}{\rm{x}} \end{align*}\)
ดังนั้น
\(\begin{align*} {{\rm{\omega }}^{\rm{2}}} &=\frac{{{\rm{k'}}}}{{\rm{m}}}{\rm{ = }}\frac{{{\rm{2k}}}}{{\rm{m}}}\\ \rm \omega &=\sqrt {\frac{{{\rm{2k}}}}{{\rm{m}}}} \end{align*}\)
| 17. | ถ้าคุณมีก้อนมวลมาตรฐาน 1 กิโลกรัม และส้อมเสียงในหน่วย Hz นอกจากนี้คุณยังมีเครื่องมือในห้องปฏิบัติการครบเซต แต่เป็นเครื่องมือที่ไม่ได้ให้ค่าในหน่วย SI และไม่ทราบค่าคงที่พื้นฐานใดๆ แล้วปริมาณใดที่สามารถวัดในหน่วย SI ได้ |
| A | ความเร่งเนื่องจากแรงโน้มถ่วง |
| B | อัตราเร็วแสงในสุญญากาศ |
| C | ความหนาแน่นของน้ำอุณหภูมิห้อง |
| D | ค่านิจสปริงของสปริงที่กำหนด |
| E | ความดันอากาศในห้อง |
ตอบ (D)
สิ่งที่รู้ในน่วย SI คือ kg , Hz หรือ s-1
(A) g หน่วย m/s2 ไม่ได้ เพราะไม่รู้ความยาวในหน่วย SI (m)
(B) c หน่วย m/s ไม่ได้ เพราะไม่รู้ความยาวในหน่วย SI (m)
(C) ρwater หน่วย kg/m3 ไม่ได้ เพราะไม่รู้ความยาวในหน่วย SI (m)
(D) k หน่วย N/m = kg/s2 = kg·Hz2 ได้ เพราะเป็นหน่วยที่รู้ทั้งหมด
(E) P หน่วย N/m2 = kg/m·s2 ไม่ได้ เพราะไม่รู้ความยาวในหน่วย SI (m)
สิ่งที่รู้ในน่วย SI คือ kg , Hz หรือ s-1
(A) g หน่วย m/s2 ไม่ได้ เพราะไม่รู้ความยาวในหน่วย SI (m)
(B) c หน่วย m/s ไม่ได้ เพราะไม่รู้ความยาวในหน่วย SI (m)
(C) ρwater หน่วย kg/m3 ไม่ได้ เพราะไม่รู้ความยาวในหน่วย SI (m)
(D) k หน่วย N/m = kg/s2 = kg·Hz2 ได้ เพราะเป็นหน่วยที่รู้ทั้งหมด
(E) P หน่วย N/m2 = kg/m·s2 ไม่ได้ เพราะไม่รู้ความยาวในหน่วย SI (m)
| 18. | ลูกตุ้มอย่างง่ายมีเชือกเบาความยาว L แขวนวัตถุมวล m กับจุดหมุนหนึ่ง และปักหมุดเล็กๆ ขวางไว้ใต้จุดหมุนที่ 2L/3 เพื่อให้ลูกตุ้มแกว่งตามรูป ถ้าจับมวลออกไป 5 องศากับแนวตั้ง แล้วปล่อยออก จะต้องใช้เวลานานเท่าใด ลูกตุ้มจึงจะกลับมาที่จุดเริ่มต้น
 |
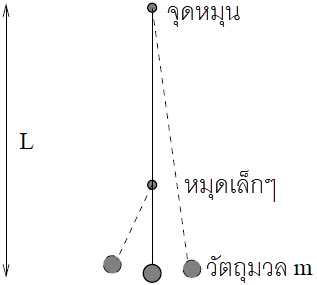| A | \(\rm\pi\sqrt{\dfrac{L}{g}}\left(1+\sqrt{\dfrac{2}{3}}\right)\) |
| B | \(\rm\pi\sqrt{\dfrac{L}{g}}\left(2+\dfrac{2}{\sqrt{3}}\right)\) |
| C | \(\rm\pi\sqrt{\dfrac{L}{g}}\left(1+\dfrac{1}{3}\right)\) |
| D | \(\rm\pi\sqrt{\dfrac{L}{g}}\left(1+\sqrt{3}\right)\) |
| E | \(\rm\pi\sqrt{\dfrac{L}{g}}\left(1+\dfrac{1}{\sqrt{3}}\right)\) |
ตอบ (E)
ให้ T1 = คาบการแกว่งรอบจุดหมุนที่อยู่สูง
และ T2 = คาบการแกว่งรอบจุดหมุนที่อยู่เตี้ย
ดังนั้น เวลาที่ใช้ในการแกว่งกลับมาที่เดิม จะเท่ากับ
ให้ T1 = คาบการแกว่งรอบจุดหมุนที่อยู่สูง
และ T2 = คาบการแกว่งรอบจุดหมุนที่อยู่เตี้ย
ดังนั้น เวลาที่ใช้ในการแกว่งกลับมาที่เดิม จะเท่ากับ
\(\dfrac{{\rm{1}}}{{\rm{2}}}{{\rm{T}}_{\rm{1}}}{\rm{ + }}\dfrac{{\rm{1}}}{{\rm{2}}}{{\rm{T}}_{\rm{2}}}=\dfrac{1}{2}\left({{\rm{2\pi }}\sqrt {\frac{{\rm{L}}}{{\rm{g}}}} {\rm{ + 2\pi \sqrt{\dfrac{L/3}{g}}}}}\right) {\rm{ = \pi }}\sqrt {\frac{{\rm{L}}}{{\rm{g}}}} \left( {{\rm{1 + }}\frac{{\rm{1}}}{{\sqrt {\rm{3}} }}} \right)\)
| 19. | ถ้ากองหลังฟุตบอลสามารถโยนลูกฟุตบอลไปได้ไกลสุด 80 เมตรตามแนวราบ แล้วลูกฟุตบอลที่ถูกโยนไปได้ไกลสุดจะมีจุดสูงสุดเท่ากับข้อใด ไม่ต้องสนแรงต้านอากาศ |
| A | 10 m |
| B | 20 m |
| C | 30 m |
| D | 40 m |
| E | 50 m |
ตอบ (B)
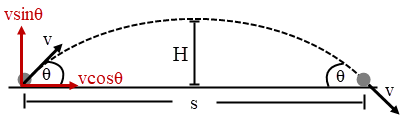พิจารณาวัตถุความเร็ว v ถูกโยนทำมุม θ กับพื้น
หาเวลาที่ใช้ในการเคลื่อนที่
จาก
ดังนั้น
หาเวลาที่ใช้ในการเคลื่อนที่
จาก
\(\begin{align*} {{\rm{s}}_{\rm{y}}} &= {{\rm{u}}_{\rm{y}}}{\rm{t}} - \frac{{\rm{1}}}{{\rm{2}}}{\rm{g}}{{\rm{t}}^{\rm{2}}}\\ 0 &= {\rm{vsin\theta t}} - \frac{{\rm{1}}}{{\rm{2}}}{\rm{g}}{{\rm{t}}^{\rm{2}}}\\ {\rm{t}} &= \frac{{2{\rm{vsin\theta }}}}{{\rm{g}}} \end{align*}\)
ดังนั้น ระยะเวลาที่วัตถุเคลื่อนที่ในแนวราบ
\({\rm{s = vcos\theta t = }}\dfrac{{{\rm{2}}{{\rm{v}}^{\rm{2}}}{\rm{sin\theta cos\theta }}}}{{\rm{g}}}{\rm{ = }}\dfrac{{{{\rm{v}}^{\rm{2}}}{\rm{sin2\theta }}}}{{\rm{g}}}\)
จะได้ว่า \({{\rm{s}}_{{\rm{max}}}}{\rm{ = }}\dfrac{{{{\rm{v}}^{\rm{2}}}}}{{\rm{g}}}\) ที่ \({\rm{2\theta = }}\dfrac{{\rm{\pi }}}{{\rm{2}}}\) หรือ \({\rm{\theta = }}\dfrac{{\rm{\pi }}}{{\rm{4}}}\)ดังนั้น
\(\begin{align*} \rm H &={{\rm{u}}_{\rm{y}}}\left( {\frac{{\rm{t}}}{{\rm{2}}}} \right) - \frac{{\rm{1}}}{{\rm{2}}}{\rm{g}}{\left( {\frac{{\rm{t}}}{{\rm{2}}}} \right)^{\rm{2}}}\\ &\rm =\left(\dfrac{v}{\sqrt2}\right)\left(\dfrac{v/\sqrt2}{g}\right)-\dfrac{1}{2}g\left(\dfrac{v/\sqrt2}{g}\right)^2\\ &= \frac{{{{\rm{v}}^{\rm{2}}}}}{{{\rm{2g}}}} - \frac{{{{\rm{v}}^{\rm{2}}}}}{{{\rm{4g}}}}\\ &= \frac{{{{\rm{v}}^{\rm{2}}}}}{{{\rm{4g}}}}\\ &= \frac{{\rm{1}}}{{\rm{4}}}{\rm{s}}\\ &= 20\,{\rm{m}} \end{align*}\)
| 20. | พิจารณาการชนแบบไม่ยืดหยุ่นสมบูรณ์ของวัตถุสองก้อน ถ้าก้อนที่ 1 มีมวล m และ เคลื่อนที่ไปทางทิศเหนือด้วยอัตราเร็ว v0 ส่วนก้อนที่ 2 มีมวล 3m เคลื่อนที่ไปทางทิศตะวันออกด้วยอัตราเร็ว v0/2 แล้วอัตราเร็วสุดท้ายหลังการชนเท่ากับข้อใด ไม่ต้องคำนึงถึงแรงโน้มถ่วง และถือว่าวัตถุทั้งสองติดไปด้วยกันหลังการชน |
| A | \(\rm7/6v_0\) |
| B | \(\rm\sqrt5/8v_0\) |
| C | \(\rm\sqrt{13}/8v_0\) |
| D | \(\rm5/8v_0\) |
| E | \(\rm\sqrt{13/8}v_0\) |
ตอบ (C)
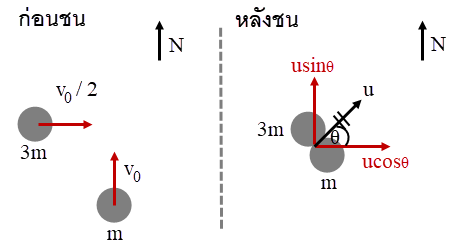ใช้กฏอนุรักษ์อนุรักษ์โมเมนตัม
แกน x
แกน x
\({\rm{3m}}\left( {\dfrac{{{{\rm{v}}_{\rm{0}}}}}{{\rm{2}}}} \right){\rm{ = (3m + m)ucos\theta }}\)
\(\dfrac{{{\rm{3}}{{\rm{v}}_{\rm{0}}}}}{{\rm{8}}}{\rm{ = ucos\theta }}\) --- (1)
แกน y
\({\rm{m}}{{\rm{v}}_{\rm{0}}}{\rm{ = (3m + m)usin\theta }}\)
\(\dfrac{{{{\rm{v}}_{\rm{0}}}}}{{\rm{4}}}{\rm{ = usin\theta }}\) --- (2)
นำ (1)2 + (2)2 จะได้
\(\begin{align*} \left( {{{\left( {\frac{3}{8}} \right)}^2}{\rm{ + }}{{\left( {\frac{1}{4}} \right)}^2}} \right){\rm{v}}_{\rm{0}}^{\rm{2}} &= {{\rm{u}}^{\rm{2}}}\\ {{\rm{u}}^{\rm{2}}} &= {\rm{v}}_{\rm{0}}^{\rm{2}}\left( {\frac{{9 + 4}}{{64}}} \right)\\ \rm u &=\frac{{\sqrt {{\rm{13}}} }}{{\rm{8}}}{{\rm{v}}_{\rm{0}}} \end{align*}\)
| 21. | ดาวสองดวงโคจรรอบมวลศูนย์กลางหนึ่ง ดังรูป โดยมวลของดาวเท่ากับ 3M และ M และดาวทั้งสองดวงห่างกัน d
 |
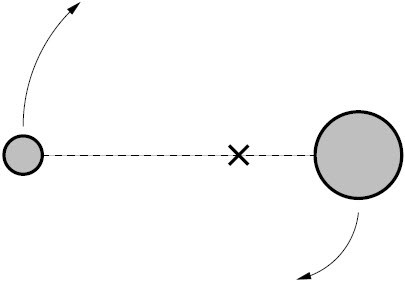| A | \(\rm-\dfrac{GM^2}{d}\) |
| B | \(\rm\dfrac{3GM^2}{d}\) |
| C | \(\rm-\dfrac{GM^2}{d^2}\) |
| D | \(\rm-\dfrac{3GM^2}{d}\) |
| E | \(\rm-\dfrac{3GM^2}{d^2}\) |
ตอบ (D)
\(\begin{align*} {\rm{V}} &= - {\rm{G}}{{\rm{m}}_{\rm{1}}}{{\rm{m}}_{\rm{2}}}{\rm{r}}\\ &= \frac{{ - {\rm{G(M)(3m)}}}}{{\rm{d}}}\\ &=\rm \frac{{ - 3G{M^2}}}{d} \end{align*}\)
| 22. | ดาวสองดวงโคจรรอบมวลศูนย์กลางหนึ่ง ดังรูป โดยมวลของดาวเท่ากับ 3M และ M และดาวทั้งสองดวงห่างกัน d
 |
| A | \(\rm \pi\sqrt{\dfrac{d^3}{GM}}\) |
| B | \(\rm \dfrac{3\pi}{4}\sqrt{\dfrac{d^3}{GM}}\) |
| C | \(\rm \pi\sqrt{\dfrac{d^3}{3GM}}\) |
| D | \(\rm 2\pi\sqrt{\dfrac{d^3}{GM}}\) |
| E | \(\rm \dfrac{\pi}{4}\sqrt{\dfrac{d^3}{GM}}\) |
ตอบ (A)
ให้ ω = อัตราเร็วเชิงมุมของดาวทั้งสอง , r1 = ระยะจากจุด cm ของ M, 3M ถึงดาวมวล M
และ r2 = ระยะจากจุด cm ของ M, 3M ถึงดาวมวล 3M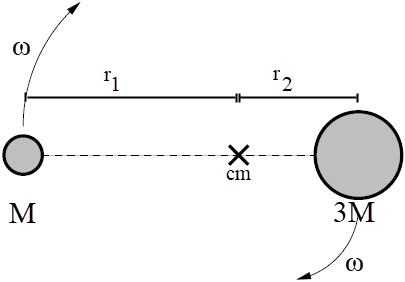
จะได้
ให้ ω = อัตราเร็วเชิงมุมของดาวทั้งสอง , r1 = ระยะจากจุด cm ของ M, 3M ถึงดาวมวล M
และ r2 = ระยะจากจุด cm ของ M, 3M ถึงดาวมวล 3M
\(\begin{array}{c} {\rm{M}}{{\rm{r}}_{\rm{1}}}{\rm{ = 3M}}{{\rm{r}}_{\rm{2}}}\\ {{\rm{r}}_{\rm{1}}}{\rm{ = 3}}{{\rm{r}}_{\rm{2}}} \end{array}\)
จาก r1 + r2 = d จะได้ว่า
\(\begin{align*} {{\rm{r}}_{\rm{1}}} &=\frac{{\rm{3}}}{{\rm{4}}}{\rm{d}}\\ {{\rm{r}}_{\rm{2}}} &=\frac{{\rm{d}}}{{\rm{4}}} \end{align*}\)
จากการเคลื่อนที่แบบวงกลมของดาวมวล 3M
\(\begin{align*} \frac{{{\rm{GM(3M)}}}}{{{{\rm{d}}^{\rm{2}}}}} &= {\rm{(3M)}}{{\rm{\omega }}^{\rm{2}}}{{\rm{r}}_{\rm{2}}}\\ \frac{{{\rm{GM}}}}{{{{\rm{d}}^{\rm{2}}}}} &= {{\rm{\omega }}^{\rm{2}}}\left( {\frac{{\rm{d}}}{4}} \right)\\ \rm \omega &= 2\sqrt {\frac{{{\rm{GM}}}}{{{{\rm{d}}^{\rm{3}}}}}} \end{align*}\)
ดังนั้น \({\rm{T = }}\dfrac{{2\pi }}{{\rm{\omega }}}{\rm{ = }}\pi \sqrt {\dfrac{{{{\rm{d}}^{\rm{3}}}}}{{{\rm{GM}}}}} \)| 23. | นำมวลติดกับสปริงอุดมคติ และสปริงมีความยาวตามปกติ ที่เวลา t = 0 มวลได้รับความเร็วต้น ถ้าคาบการสั่นแบบซิมเปิลฮาร์มอนิกเท่ากับ T แล้ว ณ เวลาใดที่สปริงจะกระทำกับมวลด้วยกำลังที่มากที่สุดเป็นครั้งแรก |
| A | t = 0 |
| B | t = T/8 |
| C | t = T/4 |
| D | t = 3T/8 |
| E | t = T/2 |
ตอบ (D)
จาก
และสมมุติให้ \({\rm{x(t) = }}{{\rm{x}}_0}\cos {\rm{\omega t}}\)
จาก
\(\begin{align*}
{{\rm{\varepsilon }}_{{\rm{spring}}}}&=\frac{{\rm{1}}}{{\rm{2}}}{\rm{k}}{{\rm{x}}^{\rm{2}}}\\
{{\rm{P}}_{{\rm{sping}}}} &=\frac{{{\rm{d}}{{\rm{\varepsilon }}_{{\rm{spring}}}}}}{{{\rm{dt}}}}\\
{{\rm{P}}_{{\rm{sping}}}}&= {\rm{ kxx'}}
\end{align*}\)
ให้ที่ t = 0 สปริงมี x'(0) = 0 และ x(0) = x0และสมมุติให้ \({\rm{x(t) = }}{{\rm{x}}_0}\cos {\rm{\omega t}}\)
\(\begin{align*}
{\rm{x'(t)}} &= - {{\rm{x}}_{\rm{0}}}{\rm{\omega sin\omega t}}\\
{\rm{xx'}} &= - {\rm{x}}_0^2{\rm{\omega sin\omega t cos\omega t}}\\
\rm P &= \rm kxx' = \frac{{ - {\rm{kx}}_0^2{\rm{\omega }}}}{2}{\rm{ sin2\omega t}}
\end{align*}\)
จะได้ Pmax เมื่อ
\(\begin{align*}
{\rm{sin2\omega t }} &= - {\rm{1}}\\
{\rm{2\omega t }} &=\frac{{3\pi }}{2},...\\
\frac{{{\rm{2\pi }}}}{{\rm{T}}}\rm t &=\frac{{3\pi }}{4},...
\end{align*}\)
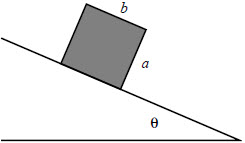
ดังนั้น \(\rm{t_{min}} = \dfrac{{3\pi }}{8}\)| 24. | บล็อกไม้สี่เหลี่ยมผืนผ้าสม่ำเสมอมวล M ยาว b สูง a อยู่พื้นเอียงดังรูป บล็อกและพื้นเอียงมีสัมประสิทธิ์แรงเสียดทาน μs และพื้นเอียงทำมุม θ กับแนวระดับ ในบางมุมวิกฤติบล็อกอาจพลิกลง หรือไถลไปตามพื้นเอียงก็ได้ จงหาความสัมพันธ์ระหว่าง a, b และ μs ที่ทำให้บล็อกพลิกลง (และไม่ไถล) ที่มุมวิกฤติ อย่าลืมว่า บล็อกเป็นรูปสี่เหลี่ยมผืนผ้า และ a ≠ b
 |
| A | μs > a/b |
| B | μs > 1 – a/b |
| C | μs > b/a |
| D | μs < a/b |
| E | μs < b/a – 1 |
ตอบ (C)
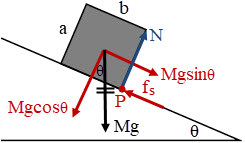จากบล็อกไม่ไถล แสดงว่า fs = Mgsinθ หรือ fs max > Mgsinθ
ให้ P เป็นจุดหมุน และเกิดทอร์กที่จุด P ที่ Critical angle torque ที่ P = 0 พอดี และ N ผ่านจุด P เนื่องจากกล่องกำลังจะพลิก จะได้ว่า
ให้ P เป็นจุดหมุน และเกิดทอร์กที่จุด P ที่ Critical angle torque ที่ P = 0 พอดี และ N ผ่านจุด P เนื่องจากกล่องกำลังจะพลิก จะได้ว่า
\(\begin{align*} {\rm{Mgsin\theta }}\left( {\frac{{\rm{a}}}{{\rm{2}}}} \right) &= {\rm{ Mgcos\theta }}\left( {\frac{{\rm{b}}}{{\rm{2}}}} \right)\\ {\rm{tan\theta}} &=\frac{{\rm{b}}}{{\rm{a}}} \end{align*}\)
แทนใน fs max > Mgsinθ จะได้
\(\begin{align*} {{\rm{\mu }}_{\rm{s}}}\rm N &> \rm Mgsin\theta\\ {{\rm{\mu }}_{\rm{s}}}{\rm{Mgcos\theta}} &> \rm Mgsin\theta\\ {{\rm{\mu }}_{\rm{s}}} &> \tan\theta\\ {{\rm{\mu }}_{\rm{s}}} &> \frac{{\rm{b}}}{{\rm{a}}} \end{align*}\)
| 25. | แผ่นดิสก์สองแผ่น มีแกนหมุนเบาเสียบที่จุดศูนย์กลางและตั้งฉากกับแผ่นพอดี โดยแกนหมุนจะต้องอยู่ในแนวตั้งตลอดเวลา และดิสก์สามารถหมุนบนแกนได้โดยไม่มีแรงเสียดทาน ถ้าดิสก์หนาเท่ากัน และทำจากวัสดุเดียวกัน แต่รัศมีแตกต่างกันเป็น r1 และ r2 ดิสก์จะมีความเร็วเชิงมุมเป็น ω1 และ ω2 ตามลำดับ เมื่อนำขอบดิสก์มาสัมผัสกัน จะเกิดแรงเสียดทานจนกระทั่งสองแผ่นหยุดชะงัก แล้วข้อใดสรุปความสัมพันธ์ที่เกิดขึ้นได้ถูกต้อง ไม่ต้องคำนึงผลที่เกิดจากแกนหมุนแนวตั้ง
 |
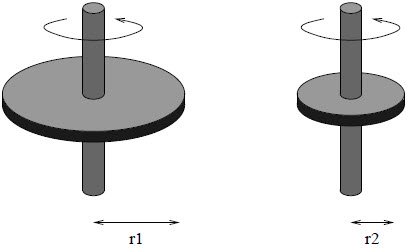| A | ω12r1 = ω22r2 |
| B | ω1r1 = ω2r2 |
| C | ω1r12 = ω2r22 |
| D | ω1r13 = ω2r23 |
| E | ω1r14 = ω2r24 |
ตอบ (D)
ให้ ρ = ความหนาแน่นของวัสดุ และ ∆t = ความหนา
เมื่อมาสัมผัสกันจะเกิดแรงเสียดทาน (f) ซึ่ง generate torque จนทำให้ทั้ง 2 แผ่นหยุดหมุนพร้อมกัน
พิจารณาแผ่นที่ 1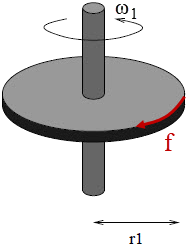
\(\begin{align*} \rm \tau_1 &=\rm \frac{\Delta L}{\Delta t}\\ \rm\int fr_1dt&=\rm 0 - \left( \frac{1}{2}m_1r_1^2 \right)\omega _1 \\ \rm-\int fr_1dt&=\rm \frac{1}{2}m_1r_1^2 \omega _1\\ \rm-\int fdt&= \frac{1}{2}\frac{{\left( {\pi \Delta {\rm{t}}\rho } \right){\rm{r}}_{\rm{1}}^{\rm{2}}{\omega _{\rm{1}}}}}{{{{\rm{r}}_{\rm{1}}}}}\\ \rm-\int fdt&= \frac{1}{2}\left( {{\rm{\pi \Delta t\rho }}} \right){\rm{r}}_{\rm{1}}^{\rm{3}}{{\rm{\omega }}_{\rm{1}}} \end{align*}\)
พิจารณาแผ่นที่ 2 ในทำนองเดียวกัน จะได้
ให้ ρ = ความหนาแน่นของวัสดุ และ ∆t = ความหนา
เมื่อมาสัมผัสกันจะเกิดแรงเสียดทาน (f) ซึ่ง generate torque จนทำให้ทั้ง 2 แผ่นหยุดหมุนพร้อมกัน
พิจารณาแผ่นที่ 1
\(\begin{align*} \rm \tau_1 &=\rm \frac{\Delta L}{\Delta t}\\ \rm\int fr_1dt&=\rm 0 - \left( \frac{1}{2}m_1r_1^2 \right)\omega _1 \\ \rm-\int fr_1dt&=\rm \frac{1}{2}m_1r_1^2 \omega _1\\ \rm-\int fdt&= \frac{1}{2}\frac{{\left( {\pi \Delta {\rm{t}}\rho } \right){\rm{r}}_{\rm{1}}^{\rm{2}}{\omega _{\rm{1}}}}}{{{{\rm{r}}_{\rm{1}}}}}\\ \rm-\int fdt&= \frac{1}{2}\left( {{\rm{\pi \Delta t\rho }}} \right){\rm{r}}_{\rm{1}}^{\rm{3}}{{\rm{\omega }}_{\rm{1}}} \end{align*}\)
พิจารณาแผ่นที่ 2 ในทำนองเดียวกัน จะได้
\(\displaystyle- \int {{\rm{fdt}} = \frac{1}{2}\left( {{\rm{\pi \Delta t\rho }}} \right){\rm{r}}_{\rm{2}}^{\rm{3}}{{\rm{\omega }}_2}} \)
ดังนั้น \({\rm{r}}_{\rm{1}}^{\rm{3}}{{\rm{\omega }}_1} = {\rm{r}}_{\rm{2}}^{\rm{3}}{{\rm{\omega }}_2}\)