หัวข้อฟิสิกส์ : มวล แรงและกฎการเคลื่อนที่
| 1. | ให้แผ่นกลม, ห่วง และทรงกลม มีมวล และรัศมีเท่ากัน และจะหมุนอย่างอิสระรอบแกนที่ผ่านจุดศูนย์กลางของวัตถุ โดยสมมุติว่าห่วงเชื่อมกับแกนหมุนด้วยซี่ล้อรถ ถ้าวัตถุที่เดิมอยู่นิ่ง ถูกกระทำที่วงด้านนอกด้วยแรงเดียวกัน ในเวลาเดียวกัน แล้วข้อใดจัดอันดับพลังงานจลน์ของวัตถุจากน้อยไปมาก หลังเวลาผ่านไป t ได้ถูกต้อง
 |
| A | แผ่นกลม, ห่วง, ทรงกลม |
| B | ทรงกลม, แผ่นกลม, ห่วง |
| C | ห่วง, ทรงกลม, แผ่นกลม |
| D | แผ่นกลม, ทรงกลม, ห่วง |
| E | ห่วง, แผ่นกลม, ทรงกลม |
ตอบ (E)
จากโจทย์ให้ทุกวัตถุถูกหมุนด้วย F เท่ากัน รัศมีเท่ากัน ดังนั้น ทอร์กต้องเท่ากัน
เนื่องจาก วัตถุที่มีโมเมนต์ความเฉื่อย (I) มาก จะหมุนช้า ทำให้พลังงานจลน์มีค่าน้อย
ดังนั้น การเรียงลำดับพลังงานจลน์จากน้อยไปมาก ต้องเรียงลำดับ I จากมากไปน้อย ดังนี้
จากโจทย์ให้ทุกวัตถุถูกหมุนด้วย F เท่ากัน รัศมีเท่ากัน ดังนั้น ทอร์กต้องเท่ากัน
เนื่องจาก วัตถุที่มีโมเมนต์ความเฉื่อย (I) มาก จะหมุนช้า ทำให้พลังงานจลน์มีค่าน้อย
ดังนั้น การเรียงลำดับพลังงานจลน์จากน้อยไปมาก ต้องเรียงลำดับ I จากมากไปน้อย ดังนี้
ห่วง (\({\rm{M}}{{\rm{R}}^{\rm{2}}}\)) , แผ่นกลม (\(\dfrac{1}{2}{\rm{M}}{{\rm{R}}^{\rm{2}}}\)) , ทรงกลม (\(\dfrac{2}{5}{\rm{M}}{{\rm{R}}^{\rm{2}}}\))
| 2. | หินหนัก 2 kg แขวนที่ปลายไม้เมตรสม่ำเสมอยาว 1 เมตร ด้วยเชือกเบา ถ้าไม้เมตรเกิดสมดุลเมื่อหินที่แขวนอยู่ อยู่ห่างจากจุดหมุนไป 0.20 m แล้วไม้เมตรมีมวลเท่าใด  |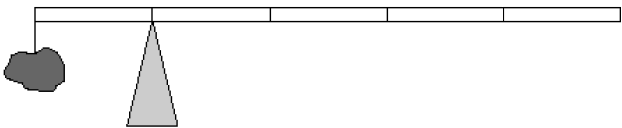
| A | 0.20 kg |
| B | 1.00 kg |
| C | 1.33 kg |
| D | 2.00 kg |
| E | 3.00 kg |
ตอบ (C)
ให้หินมีมวล m และไม้เมตรมีมวล M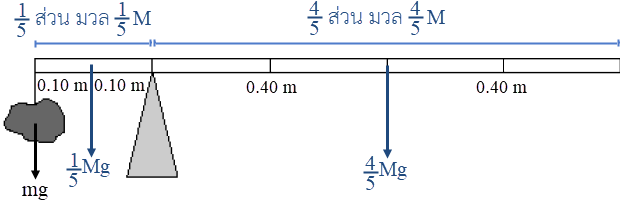
จากไม้เมตรเกิดสมดุลแสดงว่า
ให้หินมีมวล m และไม้เมตรมีมวล M
โมเมนต์ตาม \(=\) โมเมนต์ทวน
\(\begin{align*} \dfrac{4}{5}{\rm{Mg}}(0.40) &= \rm mg(0.20) + \dfrac{1}{5}{\rm{Mg}}(0.10)\\ \left( {\dfrac{4}{5}(0.40) - \dfrac{1}{5}(0.10)} \right)\rm M &= (0.20)(2)\\ \rm M &= \dfrac{4}{3} \end{align*}\)
ดังนั้น ไม้เมตรมีมวล \(\dfrac{4}{3} = 1.33 \rm ~~kg\)| 3. | ถ้าวัตถุหนึ่งเคลื่อนที่ไปตามแกน x พุ่งชนแบบยืดหยุ่นกับวัตถุแบบเดียวกันที่เดิมอยู่นิ่ง แล้วกราฟในข้อใดแสดงโมเมนตัม P เทียบกับเวลา t ของแต่ละวัตถุได้ถูกต้อง |
| A |  |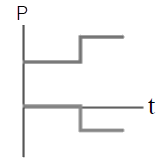
| B |  |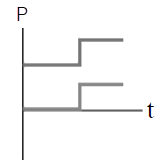
| C |  |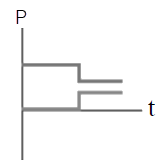
| D |  |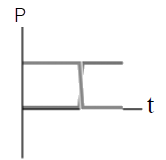
| E |  |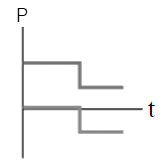
ตอบ (D)
โจทย์ให้เป็นการชนแบบยืดหยุ่นแสดงว่า
1) อนุรักษ์โมเมนตัม \(\sum \rm P\) ก่อนชน = \(\sum \rm P\)หลังชน
2) อนุรักษ์พลังงาน \(\rm E\)ก่อน = \(\rm E\)หลัง
พิจารณาจากเงื่อนไข 1)
จากกราฟจะเห็นว่า กราฟ (B), (E) มีการเปลี่ยนแปลงหลังชนไปในทำนองเดียวกัน (เพิ่มขึ้นเหมือนกัน หรือลดลงเหมือนกัน) ซึ่งขัดกับการอนุรักษ์โมเมนตัม
ดังนั้น กราฟ (B), (E) ไม่ใช่คำตอบ
และเมื่อวาดรูปจากกราฟ (A) จะได้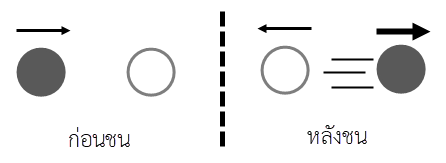
สังเกตว่า วัตถุที่อยู่นิ่งไม่ควรเด้งกลับหลังถูกชน
ดังนั้น กราฟ (A) ไม่ใช่คำตอบ
พิจารณาจากเงื่อนไข 2)
จากกราฟ (C)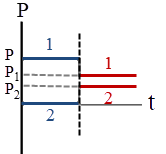
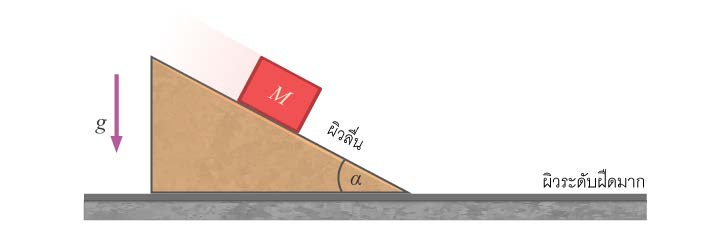
จากกราฟ (D)
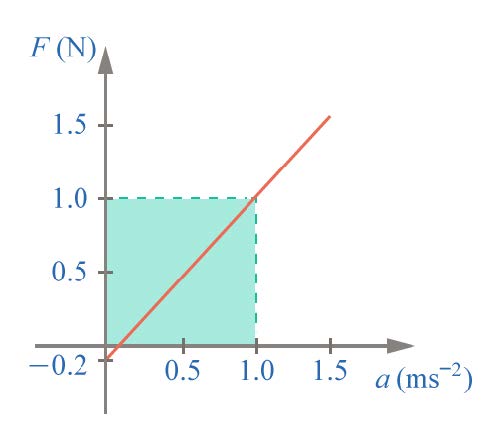
ดังนั้น กราฟ (D) ถูกต้อง
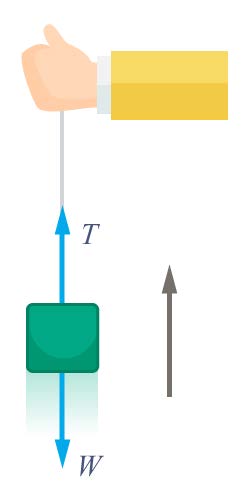
โจทย์ให้เป็นการชนแบบยืดหยุ่นแสดงว่า
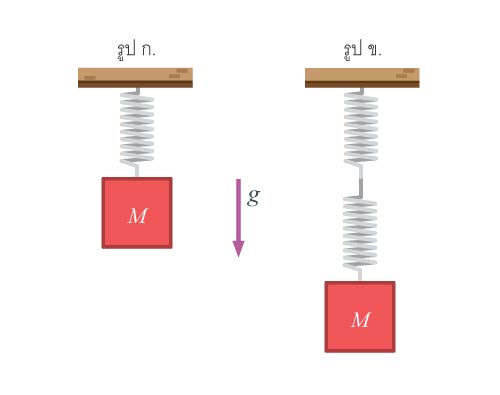
1) อนุรักษ์โมเมนตัม \(\sum \rm P\) ก่อนชน = \(\sum \rm P\)หลังชน
2) อนุรักษ์พลังงาน \(\rm E\)ก่อน = \(\rm E\)หลัง
พิจารณาจากเงื่อนไข 1)
จากกราฟจะเห็นว่า กราฟ (B), (E) มีการเปลี่ยนแปลงหลังชนไปในทำนองเดียวกัน (เพิ่มขึ้นเหมือนกัน หรือลดลงเหมือนกัน) ซึ่งขัดกับการอนุรักษ์โมเมนตัม
ดังนั้น กราฟ (B), (E) ไม่ใช่คำตอบ
และเมื่อวาดรูปจากกราฟ (A) จะได้
ดังนั้น กราฟ (A) ไม่ใช่คำตอบ
พิจารณาจากเงื่อนไข 2)
จากกราฟ (C)
\(\rm E\)ก่อน \(=\dfrac{1}{2}{\rm{m}}{{\rm{v}}^2} + 0 = \dfrac{1}{2}\dfrac{{{{\rm{m}}^2}{{\rm{v}}^2}}}{{\rm{m}}} = \dfrac{1}{2}\dfrac{{{{\rm{P}}^2}}}{{\rm{m}}}\)
\(\rm E\)หลัง \(=\dfrac{1}{2}{\rm{mv}}_1^2 + \dfrac{1}{2}{\rm{mv}}_2^2 = \dfrac{1}{2}\dfrac{{{\rm{P}}_1^{^2}}}{{\rm{m}}} + \dfrac{1}{2}\dfrac{{{\rm{P}}_2^{^2}}}{{\rm{m}}} = \dfrac{1}{{2{\rm{m}}}}\left( {{\rm{P}}_1^{^2} + {\rm{P}}_2^{^2}} \right)\)
จากกราฟสังเกตว่า \(\rm P_1 + P_2 \approx P\) แสดงว่า
\(\rm E\)ก่อน \(\approx \dfrac{1}{{2{\rm{m}}}}{\left( {{{\rm{P}}_1} + {{\rm{P}}_2}} \right)^2} = \dfrac{1}{{2{\rm{m}}}}({\rm{P}}_1^2 + {\rm{P}}_2^2 + 2{{\rm{P}}_1}{{\rm{P}}_2}) > \) \(\rm E\)หลัง
ซึ่งขัดกับการอนุรักษ์พลังงาน ดังนั้น กราฟ (C) ไม่ใช่คำตอบจากกราฟ (D)
\(\rm E\)ก่อน \(= \dfrac{1}{2}{\rm{m}}{{\rm{v}}^2} + 0 = \dfrac{1}{2}\dfrac{{{{\rm{P}}^2}}}{{\rm{m}}}\)
\(\rm E\)หลัง \(= 0 + \dfrac{1}{2}{\rm{m}}{{\rm{v}}^2} = \dfrac{1}{2}\dfrac{{{{\rm{P}}^2}}}{{\rm{m}}}\)
ซึ่ง \(\rm E\)ก่อน = \(\rm E\)หลังดังนั้น กราฟ (D) ถูกต้อง
| 4. | ให้อัตราเร็วของรถยนต์ที่มีระบบขับเคลื่อนล้อหลังมีขนาดเพิ่มขึ้น แล้วทิศทางของแรงเสียดทานบนยางรถยนต์จะเป็นไปตามข้อใด |
| A | ที่ล้อหน้ามีทิศถอยหลัง ที่ล้อหลังมีทิศไปข้างหน้า |
| B | ที่ล้อหน้ามีทิศไปข้างหน้า ที่ล้อหลังมีทิศถอยหลัง |
| C | ทุกล้อมีทิศไปข้างหน้า |
| D | ทุกล้อมีทิศถอยหลัง |
| E | แรงเสียดทานเป็นศูนย์ |
ตอบ (A)
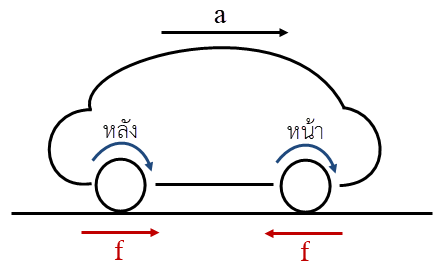ล้อหลัง : จะตะกุยพื้นเพื่อดันรถไปข้างหน้า ทำให้ล้อที่สัมผัสพื้นเคลื่อนที่ไปด้านหลัง \((\leftarrow)\) เทียบกับพื้น
ดังนั้น f ที่ต้านการเคลื่อนที่ของล้อหลังจะมีทิศไปข้างหน้า \((\rightarrow)\)
ล้อหน้า : เพลาของล้อหน้าจะเคลื่อนที่ไปข้างหน้า \((\rightarrow)\) ทำให้ล้อส่วนที่สัมผัสพื้นเคลื่อนที่ตามเพลา คือ ไปข้างหน้า \((\rightarrow)\) เทียบกับพื้น
ดังนั้น f ที่ต้านการเคลื่อนที่ของล้อหน้าจะมีทิศไปข้างหลัง \((\leftarrow)\)
ดังนั้น f ที่ต้านการเคลื่อนที่ของล้อหลังจะมีทิศไปข้างหน้า \((\rightarrow)\)
ล้อหน้า : เพลาของล้อหน้าจะเคลื่อนที่ไปข้างหน้า \((\rightarrow)\) ทำให้ล้อส่วนที่สัมผัสพื้นเคลื่อนที่ตามเพลา คือ ไปข้างหน้า \((\rightarrow)\) เทียบกับพื้น
ดังนั้น f ที่ต้านการเคลื่อนที่ของล้อหน้าจะมีทิศไปข้างหลัง \((\leftarrow)\)
| 5. | ให้แผ่นกลมสม่ำเสมอ (I = \(\dfrac{1}{2}\)MR2) มีมวล 8.0 kg สามารถหมุนรอบแกนโดยไม่มีแรงเสียดทาน และมีเชือกคล้องผ่านแผ่นกลมนั้น และแขวนมวล 6.0 kg เอาไว้ ดังรูป ถ้าเชือกไม่มีการไถล แล้วแรงตึงเชือกขณะมวลหย่อนลงมาเท่ากับข้อใด
 |
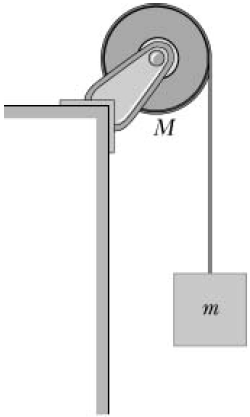| A | 20.0 N |
| B | 24.0 N |
| C | 34.3 N |
| D | 60.0 N |
| E | 80.0 N |
ตอบ (B)
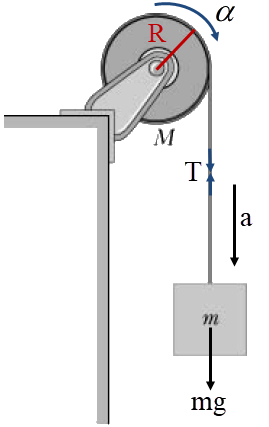โจทย์ให้ \(\rm M = 8.0 kg ,~ m = 6.0 kg\) ให้เชือกมีแรงตึง \(\rm T\)
พิจารณามวล \(\rm M\)
จาก \(\sum {\tau = {\rm{I}}\alpha }\)
จาก \(\sum {{\rm{F = ma}}}\)
พิจารณามวล \(\rm M\)
จาก \(\sum {\tau = {\rm{I}}\alpha }\)
\(\begin{align*} \rm TR &= \dfrac{{\rm{1}}}{{\rm{2}}}{\rm{M}}{{\rm{R}}^{\rm{2}}}\alpha \\ \alpha &= \dfrac{{{\rm{2T}}}}{{{\rm{MR}}}} \end{align*}\)
จากเงื่อนไขเชือกไม่ไถลทำให้
\(\rm a = \alpha \rm R = \left( {\dfrac{{{\rm{2T}}}}{{{\rm{MR}}}}} \right){\rm{R}} = \dfrac{{{\rm{2T}}}}{{\rm{M}}}\)
พิจารณามวล \(\rm m\)จาก \(\sum {{\rm{F = ma}}}\)
\({\rm{mg}} - {\rm{T = ma}}\)
แทน \({\rm{a = }}\dfrac{{{\rm{2T}}}}{{\rm{M}}}\) จะได้
\(\begin{align*} \rm mg - T &= m \dfrac{{{\rm{2T}}}}{{\rm{M}}}\\ \rm T &=\dfrac{{{\rm{mg}}}}{{1 + \dfrac{{{\rm{2m}}}}{{\rm{M}}}}}\\ &= \dfrac{{{\rm{6}}{\rm{.0(10)}}}}{{1 + \dfrac{{{\rm{2(6}}{\rm{.0)}}}}{{8.0}}}}\\ &= 24\,\,{\rm{N}} \end{align*}\)
ดังนั้น \(\rm T = 24 ~~N\)| 6. | ให้ลูกเบสบอลตกใส่ด้านบนของลูกบาส ขณะที่ลูกบาสกระแทกพื้นแล้วกระเด้งกลับด้วยอัตราเร็ว 4.0 m/s และพุ่งชนกับลูกเบสบอลที่ตกลงมาด้วยอัตราเร็ว 4.0 m/s หลังการชนลูกเบสบอลพุ่งกลับขึ้นไป ดังรูป และลูกบาสกลับมาอยู่นิ่งทันทีหลังการชน ถ้าลูกเบสบอลมวล 0.2 kg และลูกบาสมวล 0.5 kg และไม่สนแรงต้านอากาศ ไม่สนการดลเนื่องจากแรงโน้มถ่วง เพราะช่วงเวลาในการชนนั้นสั้นมาก แล้วอัตราเร็วของลูกเบสบอลหลังการชนกับลูกบาสที่พุ่งขึ้นมาเท่ากับข้อใด
 |
| A | 4.0 m/s |
| B | 6.0 m/s |
| C | 8.0 m/s |
| D | 12.0 m/s |
| E | 16.0 m/s |
ตอบ (B)
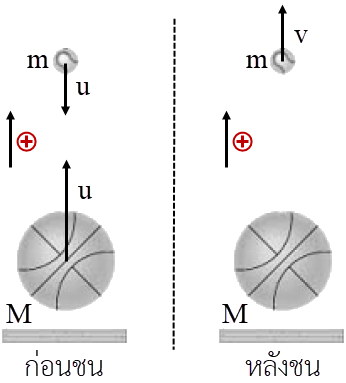โจทย์ให้ M = 0.5 kg, m = 0.2 kg, u = 4.0 m/s
ใช้หลักการอนุรักษ์โมเมนตัม (ในแนวดิ่ง)
ใช้หลักการอนุรักษ์โมเมนตัม (ในแนวดิ่ง)
ก่อนชน = หลังชน
\(\begin{align*} {\rm{Mu}} - {\rm{mu}} &= \rm M(0) + mv\\ {\rm{Mu}} - {\rm{mu}} &= \rm mv\\ v &= \left( {\frac{{{\rm{M}} - {\rm{m}}}}{{\rm{m}}}} \right){\rm{u}}\\ &= \left( {\frac{{0.5 - 0.2}}{{0.2}}} \right)4.0\\ &= 6.0\,\,{\rm{m/s}} \end{align*}\)
\(\begin{align*} {\rm{Mu}} - {\rm{mu}} &= \rm M(0) + mv\\ {\rm{Mu}} - {\rm{mu}} &= \rm mv\\ v &= \left( {\frac{{{\rm{M}} - {\rm{m}}}}{{\rm{m}}}} \right){\rm{u}}\\ &= \left( {\frac{{0.5 - 0.2}}{{0.2}}} \right)4.0\\ &= 6.0\,\,{\rm{m/s}} \end{align*}\)
| 7. | ให้วัตถุเล็กๆ ถูกขว้างไปออกจากตึกสูง 50.0 m ตามแนวนนอนด้วยอัตราเร็วต้น 10.0 m/s ตามแนววิถีที่วัตถุเคลื่อนที่ไปจะมีองค์ประกอบที่เป็นความเร่งที่สัมผัสกับแนววิถีการเคลื่อนที่ และความเร่งที่ตั้งฉากกับแนววิถี แล้วความเร่งของวัตถุในแนวสัมผัสกับแนวตั้งฉากจะมีค่าเท่ากัน หลังวัตถุถูกโยนออกไปกี่วินาที ไม่ต้องคำนึงถึงแรงต้านอากาศ |
| A | 2.00 s |
| B | 1.50 s |
| C | 1.00 s |
| D | 0.50 s |
| E | ที่ความสูงนั้นยังไม่สามารถทำให้เกิดเหตุการณ์นั้นได้ |
ตอบ (A)
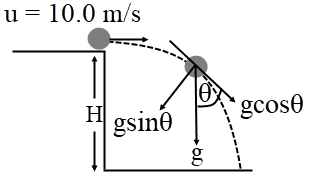จากรูป ความเร่งในแนวตั้งฉาก \(= \rm g\sin\theta\) และ ความเร่งในแนวสัมผัส \(=\rm g\cos\theta\)
โดยความเร่งในแนวตั้งฉาก \(=\) ความเร่งในแนวสัมผัส เมื่อ \(\rm g\sin\theta = g\cos\theta\)
ดังนั้น \(\tan\theta = 1\)
แสดงว่า \(\dfrac{{\rm{u}}}{{\rm{v}}} = \tan {\rm{\theta }} = 1\) ด้วย เมื่อ \(v\) เป็นความเร็วในแนวดิ่งของวัตถุ
จาก \(\rm v = gt\)
จาก
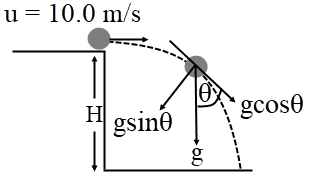
โดยความเร่งในแนวตั้งฉาก \(=\) ความเร่งในแนวสัมผัส เมื่อ \(\rm g\sin\theta = g\cos\theta\)
ดังนั้น \(\tan\theta = 1\)
แสดงว่า \(\dfrac{{\rm{u}}}{{\rm{v}}} = \tan {\rm{\theta }} = 1\) ด้วย เมื่อ \(v\) เป็นความเร็วในแนวดิ่งของวัตถุ
จาก \(\rm v = gt\)
\({\rm{t = }}\dfrac{{\rm{v}}}{{\rm{g}}}{\rm{ = }}\dfrac{{\rm{u}}}{{\rm{g}}} \approx \dfrac{{10.0}}{{10.0}} = 1.00\,\,{\rm{s}}\)
ตรวจสอบระยะทางที่ตก (s) จาก
\({\rm{s = }}\dfrac{{\rm{1}}}{{\rm{2}}}{\rm{g}}{{\rm{t}}^{\rm{2}}}{\rm{ = }}\dfrac{{\rm{1}}}{{\rm{2}}}{\rm{ \times 10 \times }}{{\rm{1}}^{\rm{2}}}{\rm{ = 5m < 50}}{\rm{.0m}}\)
ดังนั้น ความสูงเพียงพอที่จะทำให้เกิดเหตุการณ์นั้นได้| 8. | ก้อนน้ำแข็งเล็กๆ ที่เดิมอยู่นิ่ง ไหลลงมาตามแผ่นน้ำแข็งโค้งที่ไม่มีแรงเสียดทาน ดังรูป แล้วที่จุด A จะเป็นจุดเชื่อมแผ่นน้ำแข็งกับพื้นเอียงที่ยกขึ้นมา 30° จากแนวระดับ และมีสัมประสิทธิ์เสียดทาน μk ความยาวทางลาดยาว \(\dfrac{3}{2}\rm h\) ถ้าก้อนน้ำแข็งนิ่งสนิทที่ปลายด้านล่างของพื้นเอียง แล้ว μk เท่ากับข้อใด
 |
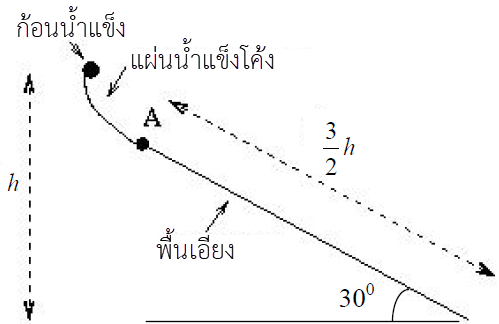| A | 0.866 |
| B | 0.770 |
| C | 0.667 |
| D | 0.385 |
| E | 0.333 |
ตอบ (B)
จากงานและพลังงาน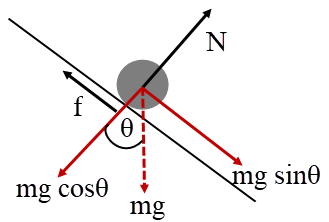
โดย \({\rm{f}} = {{\rm{\mu }}_{\rm{k}}}{\rm{N}} = {{\rm{\mu }}_{\rm{k}}}{\rm{mg}}\cos \theta \) จะได้ว่า
จากงานและพลังงาน
พลังงานศักย์โน้มถ่วง \(+\) งานที่แรงเสียดทานทำ (ติดลบ) \(= 0\) (น้ำแข็งหยุดนิ่งที่ปลายราง)
\(\rm mgh + \left( – f\left( {\dfrac{3}{2}{\rm{h}}} \right) \right)= 0\)
วาดรูปจากโจทย์
\(\rm mgh + \left( – f\left( {\dfrac{3}{2}{\rm{h}}} \right) \right)= 0\)
\(\begin{align*} \rm mgh &=\dfrac{{\rm{3}}}{{\rm{2}}}{\rm{fh}}\\ \rm mg &= \dfrac{{\rm{3}}}{{\rm{2}}}{\rm{(}}{{\rm{\mu }}_{\rm{k}}}{\rm{mg ~cos}}\theta {\rm{)}}\\ {{\rm{\mu }}_{\rm{k}}} &= \dfrac{{\rm{2}}}{{\rm{3}}}\dfrac{1}{{{\rm{cos30}}^\circ }}\\ &= \dfrac{4}{{3\sqrt 3 }}\\ &\approx 0.770 \end{align*}\)
| 9. | ให้สปริงที่ไม่ได้เป็นไปตาม กฎของฮุค มีแรง F = – kx2 โดย k เป็นค่านิจสปริง x เป็นระยะสปริงที่ยังไม่ถูกยืดจากระบบที่แสดง ดังรูป ถ้านำวัตถุมวล m ติดกับสปริงที่เดิมอยู่นิ่ง แล้วระยะยืดของสปริงจนระบบหยุดนิ่งชั่วขณะเท่ากับข้อใด สมมุติว่า ทุกพื้นผิวและรอกไม่มีแรงเสียดทาน
 |
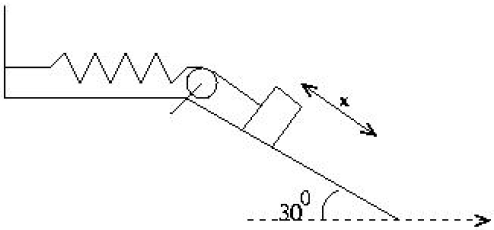| A | \(\rm \left(\dfrac{3mg}{2k}\right)^{1/2}\) |
| B | \(\rm \left(\dfrac{mg}{k}\right)^{1/2}\) |
| C | \(\rm \left(\dfrac{2mg}{k}\right)^{1/2}\) |
| D | \(\rm \left(\dfrac{\sqrt3mg}{2k}\right)^{1/2}\) |
| E | \(\rm \left(\dfrac{3\sqrt3mg}{2k}\right)^{1/2}\) |
ตอบ (A)
จากโจทย์บอกระบบหยุดนิ่งชั่วขณะ แสดงว่าตอนนั้นระบบต้องไม่มีพลังงานจลน์
สมมุติให้วัตถุเคลื่อนที่ไปได้ระยะทาง x
ตอนสุดท้าย
เพิ่มเติม ข้อนี้ใช้สมดุลแรงไม่ได้ เพราะ ตรงจุดนี้วัตถุยังมีความเร็วอยู่ (Ek ≠ 0)
จากโจทย์บอกระบบหยุดนิ่งชั่วขณะ แสดงว่าตอนนั้นระบบต้องไม่มีพลังงานจลน์
สมมุติให้วัตถุเคลื่อนที่ไปได้ระยะทาง x
ตอนสุดท้าย
Eสปริง \(\displaystyle = - \int {{\rm{Fdx}} = - \left( { - \int {{\rm{k}}{{\rm{x}}^{\rm{2}}}{\rm{dx}}} } \right){\rm{ = }}\dfrac{{\rm{1}}}{{\rm{3}}}{\rm{k}}{{\rm{x}}^{\rm{3}}}} \)
ตอนแรก
Eศักย์ \(= {\rm{mg ~x}}\sin 30^\circ = \dfrac{1}{2}{\rm{mg ~x}}\)
จากกฎอนุรักษ์พลังงาน
\(\begin{align*} \dfrac{1}{3}{\rm{k}}{{\rm{x}}^3} &= \dfrac{1}{2}{\rm{mgx}}\\ \rm x &= \sqrt {\dfrac{3}{2}\dfrac{{{\rm{mg}}}}{{\rm{k}}}} \end{align*}\)
ดังนั้น ระยะยืดเท่ากับ \({\left( {\dfrac{{3{\rm{mg}}}}{{2{\rm{k}}}}} \right)^{\frac{1}{2}}}\) เพิ่มเติม ข้อนี้ใช้สมดุลแรงไม่ได้ เพราะ ตรงจุดนี้วัตถุยังมีความเร็วอยู่ (Ek ≠ 0)
Ek = Eศักย์ – Eสปริง = \(\dfrac{1}{2}{\rm{mg x}} - \dfrac{{\rm{1}}}{{\rm{3}}}{\rm{k}}{{\rm{x}}^{\rm{3}}} = \sqrt {\dfrac{1}{8}\dfrac{{{{\rm{m}}^{\rm{3}}}{{\rm{g}}^{\rm{3}}}}}{{\rm{k}}}} - \sqrt {\dfrac{1}{{24}}\dfrac{{{{\rm{m}}^{\rm{3}}}{{\rm{g}}^{\rm{3}}}}}{{\rm{k}}}} \ne 0\)
เพราะ สมดุลแรงบอกแค่ว่า a = 0 ไม่ได้บอกว่า v = 0 หรือไม่| 10. | จุดมวลเล็กๆ เคลื่อนที่ไปตามแนวนอนระหว่างผนังสองด้านที่ไม่มีแรงเสียดทาน ด้วยพลังงานจลน์เริ่มต้น E ทุกครั้งที่ชนกับผนัง มวลจะสูญเสียพลังงานจลน์ไป \(\dfrac{1}{2}\) ไปเป็นพลังงานความร้อน แล้ววัตถุจะชนกับผนังได้กี่ครั้ง ก่อนที่ความเร็วของมวลจะลดลงจนเหลือ \(\dfrac{1}{8}\) เท่าของของเดิม |
| A | 3 |
| B | 4 |
| C | 6 |
| D | 8 |
| E | 16 |
ตอบ (C)
จาก
v2, E2 เป็นความเร็ว (ที่ลดลงไป 8 เท่า) และพลังงาน ณ ขณะนั้น
จะได้
ดังนั้น ต้องชน 6 ครั้ง
\(\begin{array}{l} {{\rm{E}}_{\rm{k}}} = \dfrac{1}{2}{\rm{m}}{{\rm{v}}^2}\\ {{\rm{E}}_{\rm{k}}} \propto {{\rm{v}}^2} \end{array}\)
ให้ v1, E1 เป็นความเร็วและพลังงานตอนแรกv2, E2 เป็นความเร็ว (ที่ลดลงไป 8 เท่า) และพลังงาน ณ ขณะนั้น
จะได้
\(\rm \displaystyle \frac{{{E_2}}}{{{E_1}}} = \frac{{v_2^2}}{{v_1^2}} = {\left( {\frac{1}{8}} \right)^2} = {\left( {\frac{1}{2}} \right)^6}\)
| 11. | คาบการแกว่งของนาฬิกาลูกตุ้มอย่างง่ายที่ลวดแขวนยาวขึ้นเพราะอุณหภูมิเพิ่มขึ้น กำหนด ก. คาบ T ของนาฬิกาลูกตุม้ อย่างง่ายเป็นไปตามสูตร \(\text{T} = 2π \sqrt{l/\text{g}}\) เมื่อ l เป็นความยาวของลวดแขวนลูกตุ้มและ g เป็นขนาดความเร่งเนื่องจากแรงโน้มถ่วงของโลก
ข. สัมประสิทธิ์การขยายตัวเชิงเส้นเนื่องจากความร้อน α คือ อัตราส่วนความยาวที่เปลี่ยนไป Δl ต่อความยาวเดิม l เมื่ออุณหภูมิเปลี่ยนไปหนึ่งหน่วย
ค. นักเรียนสามารถใช้การประมาณ \(\rm \sqrt{1+x}≈1 + x/2\) เมื่อ x มีขนาดน้อย 1 กว่ามาก ๆ
นาฬิกาลูกตุ้ม อย่างง่ายเรือนหนึ่งมีลวดแขวนที่มีสัมประสิทธิ์การขยายตัว เชิงเส้นเนื่องจากความร้อนเท่ากับ α และมีคาบแกว่ง T ที่ความยาว l1 เมื่ออุณหภูมิเพิ่มขึ้น Δθ น้อยมาก ๆ เมื่อ เทียบกับอุณหภูมิเดิม และคาบการแกว่งเปลี่ยนไปเป็น T + ΔT จงหาค่าอัตราส่วน ΔT/T ในรูปของตัวแปรที่กำหนดมา(ข้อสอบคัดเลือก ม.4 ศูนย์เตรียม 2 ก.ย. 2550) |
| 12. | มวล M กับ m เชื่อมกันด้วยสปริงเบา ๆ กำลังสั่น "อยู่กับที่" เทียบกับระบบอ้างอิงเฉื่อย โดยที่ m สั่นด้วยแอมพลิจูด A จงหาค่าของแอมพลิจูดของการสั่นของ M (ข้อสอบคัดเลือก ม.5 ศูนย์เตรียม 26 ส.ค. 2555)  |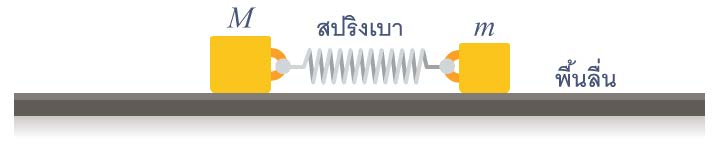
| 13. |  (ข้อสอบคัดเลือก ม.5 ศูนย์เตรียม 31 ส.ค. 2557) |
| 14. | การเคลื่อนที่ของระบบนี้บรรยายได้ด้วยการเคลื่อนที่ 3 สมการ
\(\rm m\ddot x_1 = +k(x_2 − x_1 − ℓ)\) . . . (1)
จงเขียนอีก 2 สมการให้ครบแล้วแก้สมการเพื่อหาความถี่ของการสั่นพื้นฐานซึ่งมีอยู่ 2 ค่า(ข้อสอบปลายค่าย 2 ม.5 ศูนย์เตรียม 26 มี.ค. 2556)  |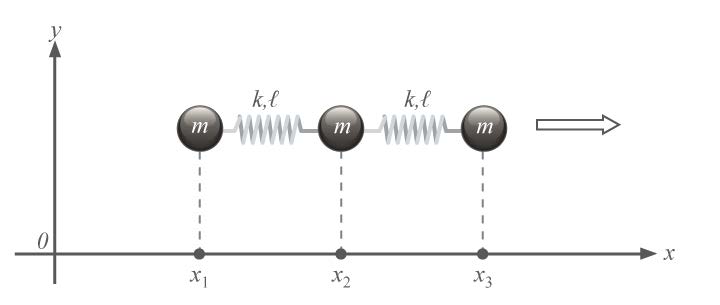
ตอบ
\(\rm m\ddot x_2 = +k(x_3-x_2 − ℓ)-k(x_2-x_1 − ℓ)\) . . . (2)
\(\rm m\ddot x_3 = -k(x_3-x_2 − ℓ)\) . . . (3)
\(\rm ω_2=\sqrt{\dfrac{3k}{m}}\)
\(\rm f_2 = \dfrac{1}{2\pi}\sqrt{\dfrac{3k}{m}}\)
\(\rm m\ddot x_2 = +k(x_3-x_2 − ℓ)-k(x_2-x_1 − ℓ)\) . . . (2)
\(\rm m\ddot x_3 = -k(x_3-x_2 − ℓ)\) . . . (3)
\(\rm ω_2=\sqrt{\dfrac{3k}{m}}\)
\(\rm f_2 = \dfrac{1}{2\pi}\sqrt{\dfrac{3k}{m}}\)
| 15. | ล้อทรงกระบอกตันมวล M รัศมี R สามารถหมุนได้คล่องรอบจุด O มีปลายหนึ่งของสปริง k ยึดไว้และอีกปลายของสปริงยึดกับเพดาน มวล m ซึ่งถ่วงขอบของทรงกระบอกทำให้นิ่งและ OA อยู่ในแนวระดับพอดี ต่อมาดึง m ลงนิดหน่อยแล้วปล่อย m จะเคลื่อนขึ้นลงๆ ด้วยคาบของการสั่นเป็นเท่าไร (ข้อสอบปลายค่าย 1 ม.5 ศูนย์เตรียม 24 ต.ค. 2553)  |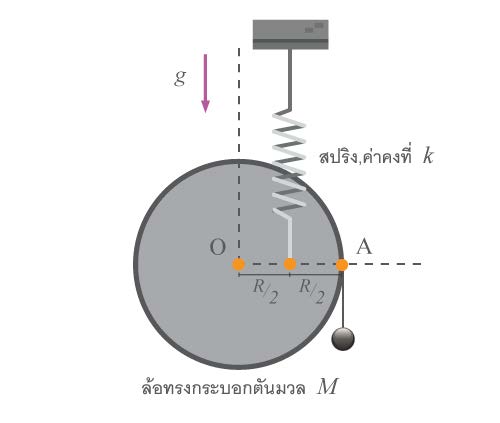
| 16. | ลูกกลมโลหะขนาดเล็กมาก 2 ลูกที่เหมือนกันทุกประการ (แต่ละลูกมีมวล m และประจุ q) ถูกแขวนจากเชือกที่ทำจากฉนวนยาว L จงหาค่า x เมื่อระบบอยู่ในสมดุล โดยมุม θ มีขนาดเล็กมากจนประมาณได้ว่า tan θ ≈ sin θ (ตอบในรูปของตัวแปร m, q, L และค่าคงที่มาตรฐานต่างๆ เช่น g) (ข้อสอบปลายค่าย 1 ม.4 ศูนย์เตรียม 18 ต.ค. 2554)  |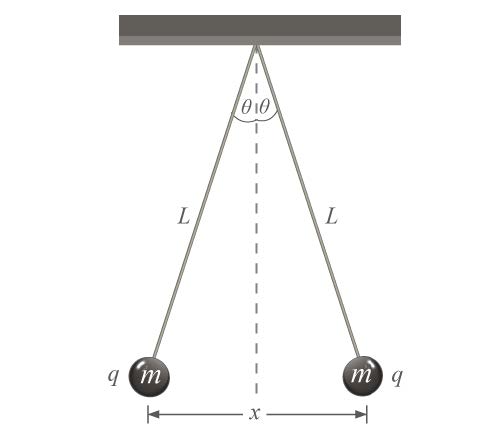
| 17. | แผ่นกลมแบนแกว่งได้คล่องในระนาบของแผ่นรอบจุด O ระยะทางจาก O ถึงจุด CM ต้องมีค่าเท่าไร คาบของการแกว่งด้วยแอมพลิจูดเล็ก ๆ จึงจะมีค่าเล็กที่สุด และค่านี้เป็นเท่าไรในรูปของ g , R (ข้อสอบปลายค่าย 2 ม.5 ศูนย์เตรียม 24 มี.ค. 2552)  |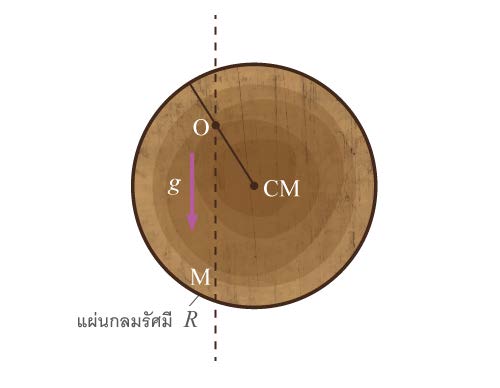
| 18. | ภาพนี้แสดงระบบในสภาวะสมดุลเชิงกล l เป็นระยะทางระหว่างรอกทั้งสอง ขณะที่เชือกส่วนนี้ทำมุม θ0 กับแนวดิ่งถ้าดึง M ลงนิดหน่อยแล้วปล่อยระบบจะสั่น ( M และ m เคลื่อนที่ขึ้นลงสลับกัน) จงวิเคราะห์หาคาบของการสั่นด้วยแอมพลิจูดเล็ก ๆ นี้ในเทอมของ m , M , l , g , sin θo (ข้อสอบคัดเลือก ม.5 ศูนย์เตรียม 31 ส.ค. 2557) หมายเหตุ \(\dfrac{1}{1+a} ≈ 1-a\) สำหรับ \(|a| ≪ 1\) \(Δ(\cos θ) ≈ −\sin θ ⋅ Δθ\) ถ้ารู้แคลคูลัส... (ไม่รู้ก็ทำได้อยู่แล้ว) |
| 19. | สปริงไร้มวล ความยาวธรรมชาติ l ค่าคงตัวสปริง k ขดหนึ่งวางตั้งตรงอยู่ในแนวดิ่ง ปลายล่างของสปริงถูกยึดไว้กับพื้น ส่วนปลายบนเคลื่อนที่ได้อย่าอิสระ ปล่อยวัตถุมวล m จากที่สูง h จากปลายบนของสปริงให้ตกในแนวดิ่ง ลงมาบนสปริงกำหนดว่าเมื่อวัตถุชนกับสปริง แล้วจะถูกยึดติดกับปลายของสปริงตลอดเวลา สมมุติด้วยว่าความสูงที่ปล่อยวัตถุลงมาไม่สูงมากพอให้สปริงหดสั้นจนถึงพื้นได ้
1) สปริงหดสั้นที่สุดเท่าใด
2) ตำแหน่งสมดุลของวัตถุอยู่สองจากพื้นเท่าใด
3) วัตถุจะกระดอนกลับขึ้นไปสูงสุดจากพื้นเท่าใด
4) วัตถุมีอัตราเร็วสูงสุดเท่าใด
5) ให้ y เป็นตำแหน่งของวัตถุจากตำแหน่งสมดุล โดยให้ y มีค่าเป็นบวกเมื่อวัดขึ้นในแนวดิ่ง ที่ตำแหน่งใด ๆ นี้วัตถุมีความเร่งเท่าใด
จงใหเ้หตุผลแสดงว่าวัตถุจะสั่นขึ้นลงแบบฮาร์มอนิกอย่างง่าย แล้วให้หาว่าตำแหน่ง y ของวัตถุจากตำแหน่งสมดุลที่เวลา t ใด ๆหลังติดกับสปริงเป็นฟังก์ชันอย่างใดของเวลา t
6) การสั่นนี้มีคาบเท่าใด
(ข้อสอบปลายค่าย 1 ม.4 ศูนย์เตรียม 24 ต.ค. 2552) |
ตอบ
1) \(\rm x =\dfrac{mg}{k}+\dfrac{\sqrt{m^2g^2 + 2mghk}}{k}\)
2) \(l-\dfrac{\text{mg}}{\text{k}}\)
3) \(\text H =l -\dfrac{\text{mg}}{\text{k}}+\dfrac{\sqrt{\rm m^2g^2 + 2mghk}}{\text k}\)
4) \(\rm v_{max} = \sqrt{\dfrac{mg^2}{k}+2gh}\)
5) \(\rm \dfrac{d^2}{dt^2}y=-\left(\dfrac{k}{m}\right)y\) และ \(\rm y(t)=\left[\dfrac{\sqrt{\rm m^2g^2 + 2mghk}}{\text k}\right]\sin\left[\sqrt{\dfrac{k}{m}}t+arcsin\left(\dfrac{mg}{\sqrt{\rm m^2g^2 + 2mghk}}\right)\right]\)
6) \(\rm T=2\pi\sqrt{\dfrac{m}{k}}\)
1) \(\rm x =\dfrac{mg}{k}+\dfrac{\sqrt{m^2g^2 + 2mghk}}{k}\)
2) \(l-\dfrac{\text{mg}}{\text{k}}\)
3) \(\text H =l -\dfrac{\text{mg}}{\text{k}}+\dfrac{\sqrt{\rm m^2g^2 + 2mghk}}{\text k}\)
4) \(\rm v_{max} = \sqrt{\dfrac{mg^2}{k}+2gh}\)
5) \(\rm \dfrac{d^2}{dt^2}y=-\left(\dfrac{k}{m}\right)y\) และ \(\rm y(t)=\left[\dfrac{\sqrt{\rm m^2g^2 + 2mghk}}{\text k}\right]\sin\left[\sqrt{\dfrac{k}{m}}t+arcsin\left(\dfrac{mg}{\sqrt{\rm m^2g^2 + 2mghk}}\right)\right]\)
6) \(\rm T=2\pi\sqrt{\dfrac{m}{k}}\)
| 20. | ในการเคลื่อนที่แบบซิมเปิลฮาร์มอนิกของวัตถุใดๆ ความเร่งของวัตถุมีเฟสนำหน้าความเร็วอยู่เท่าใด |
| 21. | การทดลองเรื่องการเคลื่อนที่แบบฮาร์มอนิกอย่างง่าย ถ้าใหลู้กตุ้มเคลื่อนที่จาก ไป ไป แล้ว ไป ดังรูปใช้เวลา วินาที คาบของการเคลื่อนที่มีค่าเท่าใด
 |
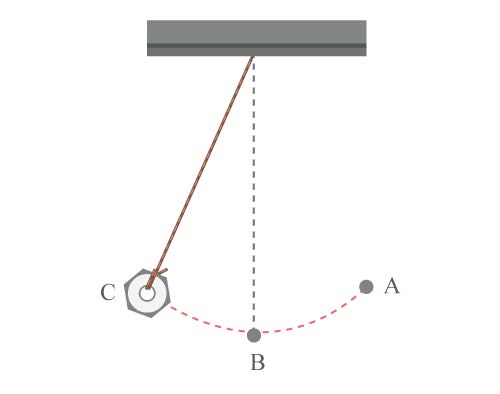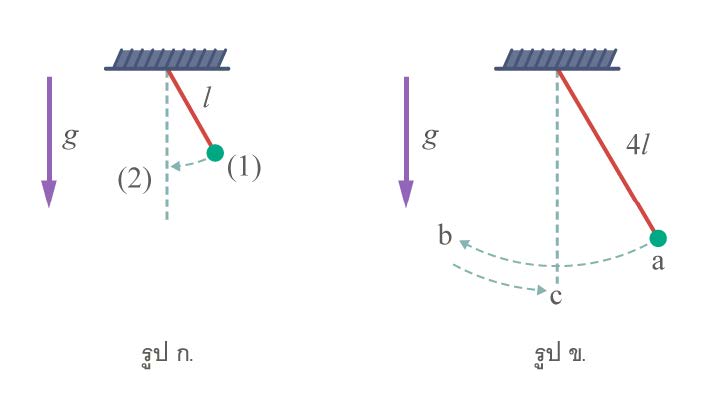
| 22. | ถ้าลูกตุ้มในรูป ก แกว่งจากตำแหน่ง (1) ไปตำแหน่ง (2) ใช้เวลา t การแกว่งในรูป ข จากตำแหน่ง a ไป b ไป c ใช้เวลาเท่าใด
 |
| 23. | จงยกตัวอย่างวัตถุที่มีการสั่นที่พบเห็นในชีวิตประจำวัน |
| 24. | มวล 400 กรัม ติดอยู่กับสปริงซึ่ง มีค่านิจสปริง 25.6 นิวตันต่อเมตร โดยเริ่มต้นดึงมวลให้ได้ระยะ 5.00 เซนติเมตร จากตำแหน่งสมดุล แล้วปล่อยให้สั่นอย่างอิสระในแนวระดับ จงหาสมการแสดงการกระจัดในช่วงเวลาต่าง ๆ ของมวลนี้
 |
| 25. | เมื่อใช้สโตรโบสโคปที่มี 1 ช่อง วัดความถี่ของการสั่นของมวล 0.25 กิโลกรัม ซึ่งผูกกับสปริงที่แขวนในแนวดิ่ง พบว่าเห็นภาพมวลหยุดนิ่งที่หนึ่งได้เมื่ออัตราเร็วของสโตรโบสโคปเป็น 3, 4 และ 12 รอบต่อวินาที ถัดกันไป ถามว่าค่านิจสปริงมีค่ากี่นิวตันต่อเมตร |
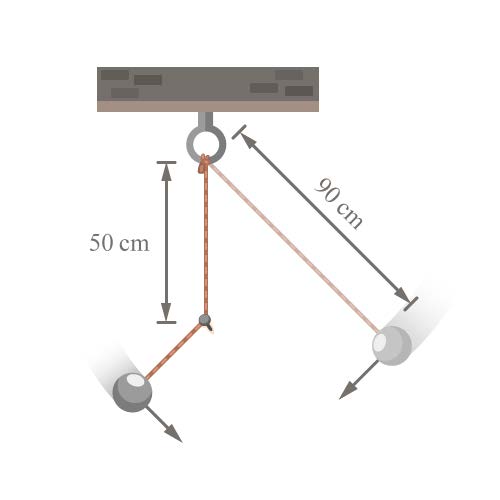
| 26. | ปล่อยลูกตุ้มซึ่งมีสายยาว 90 เซนติเมตรจากมุมหนึ่งให้แกว่ง แต่สายลูกตุ้มติดตะปูที่ระยะ 50 เซนติเมตร ใต้จุดที่แขวนในแนวดิ่งลูกตุ้มจะแกว่งกลับมาที่เดิมในเวลาเท่าใด
 |
| 27. | วัตถุเคลื่อนที่แบบฮาร์มอนิกอย่างง่าย โดยมีความสัมพันธ์ของการกระจัด (y) หน่วยเมตร และเวลา (t) หน่วยวินาที เป็นไปตามสมการ
y = 0.5 sin(10t)
อยากทราบว่าขนาดของความเร่ง ที่ตำแหน่งไกลสุดจากสมดุลมีค่าเท่าไร |
| 28. | นาฬิกาแบบลูกตุ้มเรือนหนึ่งลูกตุ้มแกว่งได้ 60 รอบต่อนาที ความยาวของก้านของลูกตุ้มนาฬิกามีค่ากี่เมตร |
| 29. | มวล M กับ m เชื่อมกันด้วยสปริงเบา ๆ กำลังสั่น "อยู่กับที่" เทียบกับระบบอ้างอิงเฉื่อย โดยที่ m สั่นด้วยแอมพลิจูด A จงหาค่าของแอมพลิจูดของการสั่นของ M (ข้อสอบคัดเลือก ม.5 ศูนย์เตรียม 26 ส.ค. 2555)  |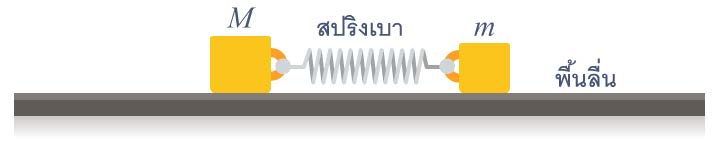
| 30. | ถ้าคุณดันหนังสือกับผนังแนวดิ่งด้วยแรงมากพอหนังสือจะไม่ไถลตกลงมา ถ้าสัมประสิทธิ์ของความเสียดทานสถิตระหว่างหนังสือกับผนังมีค่าเท่ากับ 0.7
1) คุณจะตองออกแรงดันตั้งฉากกับผนังด้วยขนาดอย่างน้อยเท่าใด หนังสือมวล 2.0 kg จึงจะไม่ไถลตกลงมากำหนดว่าความเร่งเนื่องจากแรงโน้มถ่วงโลกมีขนาด 9.8 m/s2
2) ถ้าคุณออกแรงดันขนาด 35N แรงเสียดทานสถิตที่ผนังกระทำต่อหนังสือมีขนาดเท่าใด
(ข้อสอบคัดเลือก ม.4 ศูนย์เตรียม 28 ส.ค. 2548) |
| 31. | ห่วงเล็ก ๆ คล้องอยู่ในห่วงใหญ่ดังรูป โดยที่ห่วงใหญ่มีรัศมี R ถ้าสัมประสิทธิ์ความเสียดทานของทั้งสองห่วงเท่ากับศูนย์ จงหาค่าของมุม θ ที่จุดสมดุลเมื่อห่วงใหญ่หมุนรอบตัวเองด้วยความเร็วเชิงมุม ω สูงมาก ๆ
 |
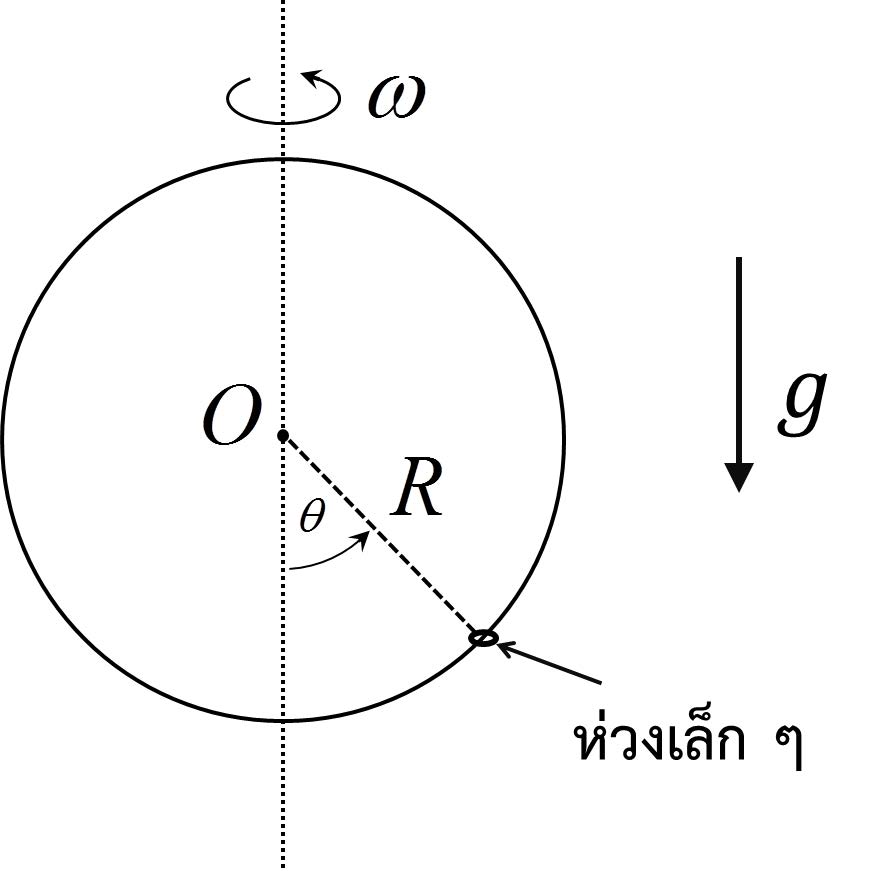| 32. | ดีดวัตถุมวล m ก้อนหนึ่งด้วยอัตราเร็วต้น u ให้ไถลขึ้นไปตามพื้นเอียงซึ่งทำมุม θ กับแนวระดับ เมื่อวัตถุขึ้นไปไดสู้งสุดก็ตกกลับมาตามพื้นเอียง ถ้าสัมประสิทธิ์ของความเสียดทานจลน์ระหว่างวัตถุกับผิวพื้นเอียงมีค่า μk อัตราเร็วของวัตถุขณะที่กลับมาถึงที่ปลายพื้นเอียงมีค่าเท่าใด (ข้อสอบคัดเลือก ม.4 ศูนย์เตรียม 3 ก.ย. 2549) |
| 33. | ตาชั่งสปริงอันหนึ่งแขวนไว้กับเพดานลิฟต์ที่กำลังเคลื่อนที่ ถ้าปลายล่างของตาชั่งมีวัตถุมวล 10 kg แขวนอยู่และตาชั่งอ่านค่าได ้125 N
1) จงหาความเร่ง (ทิศเเละขนาด) ของลิฟต์
2) ถ้าที่แขวนตาชั่งหลุดจากเพดาน ตาชั่งอ่านค่าเท่าใด
กำหนดว่าขนาดสนามโน้มถ่วงของโลกที่บริเวณนั้นมีค่าเท่ากับ 9.8 N/kg(ข้อสอบคัดเลือก ม.4 ศูนย์เตรียม 3 ก.ย. 2549) |
| 34. | ในระบบดาวฤกษ์สองดวง m1 กับ m2 ซึ่งโคจรรอบกันและกัน m1 โคจรตามแนววงกลมรัศมี R1 นั้น m2 จะมีอัตราเร็วเชิงเส้นเป็นเท่าใด (ใช้กฎการโน้มถ่วง \(\rm F =\dfrac{Gm_1m_2}{r^2} ,~ r =\) ระยะห่าง) (ข้อสอบคัดเลือก ม.4 ศูนย์เตรียม 26 ส.ค. 2555) |
| 35. | ดีดวัตถุมวล m ด้วยอัตราเร็วต้นไปในทางทิศขวามือให้ไถลไปบนผิวแผ่นไม้มวล M แผ่นไม้วางอยู่บนพื้นลื่นอีกทีหนึ่ง ให้ μk และ μs เป็นสัมประสิทธิ์ความเสียดทานจลน์และสัมประสิทธความเสียดทานสถิตระหว่างวัตถุและแผ่นไม้ตามลำดับ
1) แรงเสียดทานที่แผ่นไม้ทำต่อวัตถุมีทิศทางใด และมีขนาดเท่าใด
2) ความเร่งของแผ่นไม้มีทิศทางใด และมีขนาดเท่าใด
3) แผ่นไม้เคลื่อนที่ไปเท่าใด เมื่อวัตถุและแผ่นไม้มีความเร็วเท่ากัน
4) วัตถุไถลไปบนแผ่นไม้เป็นระยะทางเท่าใด (วัดเทียบกับแผ่นไม ้ และวัดตั้งแต่ต้นจนวัตถุเริ่มหยุดไถลบนแผ่นไม้)
5) เมื่อวัตถุหยุดไถล แรงเสียดทานที่แผ่นไม้ทำต่อวัตถุมีขนาดเท่าใด และมีทิศทางใด
(ข้อสอบคัดเลือก ม.4 ศูนย์เตรียม 29 ส.ค. 2553) |
ตอบ
1) ทิศไปทางซ้าย และ \(\rm f_k = μ_kmg\)
2) ทิศไปทางขวา และ \(\rm a = \dfrac{\mu_kmg}{M}\)
3) แผ่นไม้เคลื่อนที่ไปได้ \(\rm \dfrac{mMu^2}{2\mu_kg(m+M)^2}\)
4) วัตถุไถลไปได้ \(\rm \dfrac{Mu^2}{2\mu_k g(M+m)}\)
5) ไม่เกิดทิศ และแรงเสียดทานจลน์เท่ากับศูนย์
1) ทิศไปทางซ้าย และ \(\rm f_k = μ_kmg\)
2) ทิศไปทางขวา และ \(\rm a = \dfrac{\mu_kmg}{M}\)
3) แผ่นไม้เคลื่อนที่ไปได้ \(\rm \dfrac{mMu^2}{2\mu_kg(m+M)^2}\)
4) วัตถุไถลไปได้ \(\rm \dfrac{Mu^2}{2\mu_k g(M+m)}\)
5) ไม่เกิดทิศ และแรงเสียดทานจลน์เท่ากับศูนย์
| 36. | ท่อนผอม, ตรง, ยาว, มวล M ความยาว L กำลังล้มจากหยุดนิ่งจากแนวดิ่งบนพื้นฝืด จงวิเคราะห์หาแรงเสียดทานที่พื้นกระทำต่อปลายล่างของท่อนทำให้ท่อนไม่ไถลไปทางซ้าย หาแรงปฏิกิริยาที่พื้นกระทำต่อปลายล่าง แล้วหาเงื่อนไขเกี่ยวกับค่าสัมประสิทธิ์ความเสียดทาน (μ) ที่จะทำให้ปลายล่างไม่ไถลไปทางซ้ายเลย [ถึงแม้ว่าในที่สุดจะไปทางขวา] (ข้อสอบปลายค่าย 1 ม.5 ศูนย์เตรียม 18 ธ.ค. 2554)  |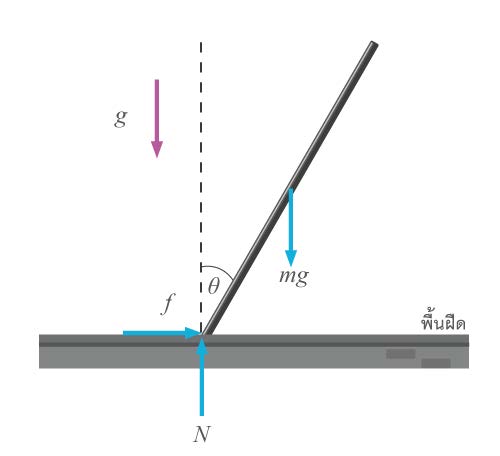
ตอบ
\(\rm f=\dfrac{3mg}{4}(3\cos\theta-2)\sin\theta\)
\(\rm N = \dfrac{3mg}{4}\left[3\cos^2\theta-2\cos\theta-1+\dfrac{4}{3}\right]\)
\(\rm \mu \approx 0.3706\) โดย \(\rm \mu \ge \dfrac{f}{N}\) ทุกๆ θ
\(\rm f=\dfrac{3mg}{4}(3\cos\theta-2)\sin\theta\)
\(\rm N = \dfrac{3mg}{4}\left[3\cos^2\theta-2\cos\theta-1+\dfrac{4}{3}\right]\)
\(\rm \mu \approx 0.3706\) โดย \(\rm \mu \ge \dfrac{f}{N}\) ทุกๆ θ
| 37. | มวล m1 , m2 โยงกันด้วยเชือกยาว ℓ กำลังตกเข้าหาโลกมวล M ในแนวเข้าสู่ O โดยไม่มีการหมุน จงหาความตึงในเส้นเชือกในเทอมของ r , m1 , m2 , M , ℓ และ G ซึ่งเป็นค่า Gravitational constant และถ้า ℓ ≪ r ความตึงนี้จะมีค่าประมาณเท่าใด (ข้อสอบปลายค่าย 2 ม.5 ศูนย์เตรียม 24 มี.ค. 2552)  |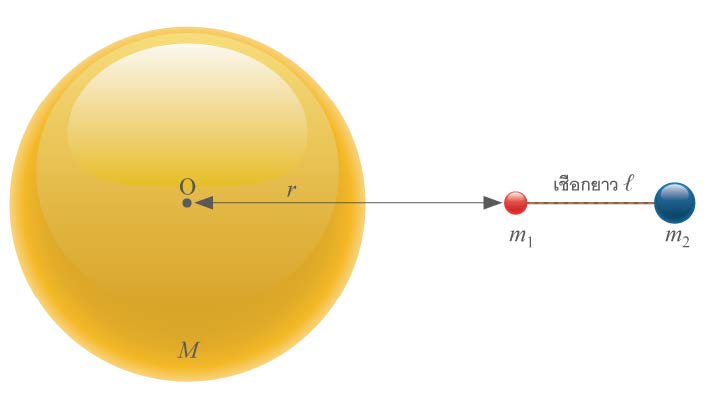
| 38. | ค่อย ๆ วางวัตถุมวล m อย่างช้าๆ ลงบนทางเลื่อน (มวลมากกว่า m มาก ๆ) ในสนามบินสุวรรณภูมิซึ่ง กำลังเลื่อนด้วยอัตราเร็ว u คงตัว ถ้าสัมประสิทธิ์ของความเสียดทานจลน์ระหว่างวัตถุและทางเลื่อนเท่ากับ μk
1) จงหา นานเท่าใดหลังจากวางวัตถุ วัตถุจึงจะหยุดไถล และ
2) วัตถุเคลื่อนที่ไปได้ระยะทางเท่าใด (เทียบกับคนที่ยืนอยู่นอกทางเลื่อน) ในระหว่างช่วงเวลาในข้อ 1)
(ข้อสอบคัดเลือก ม.4 ศูนย์เตรียม 2 ก.ย. 2550) |
| 39. | วัตถุเล็ก ๆ ตกจากหยุดนิ่งตามแนวรางลื่นจาก A ไป C แล้วไป B จะใช้เวลาเป็นกี่เท่าของการตกตามแนวรางลื่น A ตรงไป B (ข้อสอบคัดเลือก ม.4 ศูนย์เตรียม 28 ส.ค. 2554)  |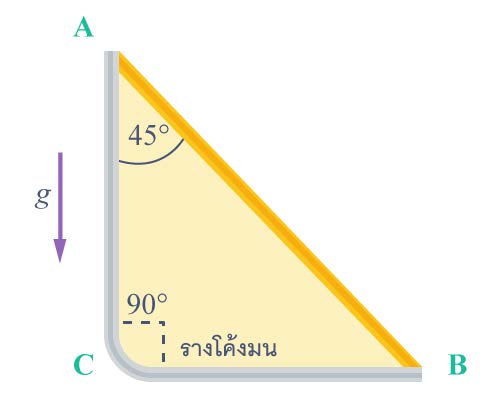
| 40. | M ถูกดีดด้วยความเร็วต้น vo ให้กระตุกโซ่ออกไปจากกองที่ origin O ของระบบอ้างอิงเฉื่อย XOY โซ่มีมวลต่อหน่วยความยาวเป็น λ สัมประสิทธิ์ความเสียดทานระหว่างโซ่และ M กับพื้นเป็น μ จงวิเคราะห์หา:
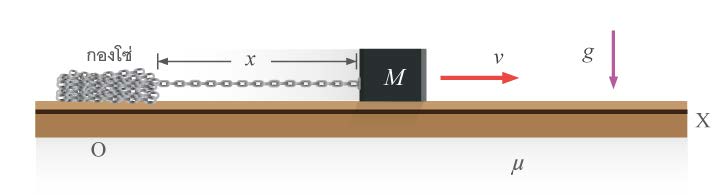 ก. สมการเคลื่อนที่ equation of motion ของ M
ข. ความเร็ว v ที่ขณะใดๆ ในรูปของ vo,M, g, μ, λ และ x
ค. ความเร่ง \(\rm\dfrac{d}{dt}v\) ในรูปของ vo,M, g, μ, λ และ x
ง. ความเร่ง \(\rm\dfrac{d}{dt}v\) ที่จังหวะที่ x = 0 เป็นเท่าใด
(ข้อสอบปลายค่าย 1 ม.5 ศูนย์เตรียม 24 ต.ค. 2548) |
ตอบ
ก. \(\rm (M + λx)\ddot{x}= −μ(M + λx)g − λv^2\)
ข. \(\rm v(x) =\sqrt{\dfrac{3λ M^2v_0^2− 2μg[(M + λx )^3- M^3]}{3λ(M + λx)^2}}\)
ค. \(\rm a = -\mu g-\dfrac{1}{3(M + λx)^3}(3λ M^2v_0^2− 2μg[(M + λx )^3- M^3])\)
ง. \(\rm a = -\mu g-\dfrac{λ}{M}v^2_0\)
ก. \(\rm (M + λx)\ddot{x}= −μ(M + λx)g − λv^2\)
ข. \(\rm v(x) =\sqrt{\dfrac{3λ M^2v_0^2− 2μg[(M + λx )^3- M^3]}{3λ(M + λx)^2}}\)
ค. \(\rm a = -\mu g-\dfrac{1}{3(M + λx)^3}(3λ M^2v_0^2− 2μg[(M + λx )^3- M^3])\)
ง. \(\rm a = -\mu g-\dfrac{λ}{M}v^2_0\)
| 41. | จงอธิบายวิธีการหาแรงลัพธ์ของแรงสามแรงที่อยู่ในแนวเดียวกันโดยวิธีการสร้างรูป ก) โดยวิธีการวาดรูป ข) โดยวิธีการคำนวณ |
ตอบ
ก) ใช้วิธีหางต่อหัว
ข) รวมขนาดของแรงโดยให้กำหนดให้แรงทิศเดียวกันมีค่าเป็นบวก ทิศตรงข้ามมีค่าเป็นลบ
ก) ใช้วิธีหางต่อหัว
ข) รวมขนาดของแรงโดยให้กำหนดให้แรงทิศเดียวกันมีค่าเป็นบวก ทิศตรงข้ามมีค่าเป็นลบ
| 42. | คนสองคนชักเย่อกัน ต่างคนต่างออกแรง F เท่ากันที่ปลายเชือกทั้งสองความตึงในเชือกมีค่าเท่าใด |
ตอบ F
ปลายเชือกทั้งสองด้านถูกดึงด้วยแรง F ทำให้เกิดแรงตึงในเชือกเท่ากับ F ด้วยเพราะปลายเชือกทั้งสองไม่ได้เคลื่อนที่ แรงตึงเชือกจึงต้องเท่ากับแรงดึง F ที่ปลายเชือกทั้งสองด้าน
ปลายเชือกทั้งสองด้านถูกดึงด้วยแรง F ทำให้เกิดแรงตึงในเชือกเท่ากับ F ด้วยเพราะปลายเชือกทั้งสองไม่ได้เคลื่อนที่ แรงตึงเชือกจึงต้องเท่ากับแรงดึง F ที่ปลายเชือกทั้งสองด้าน
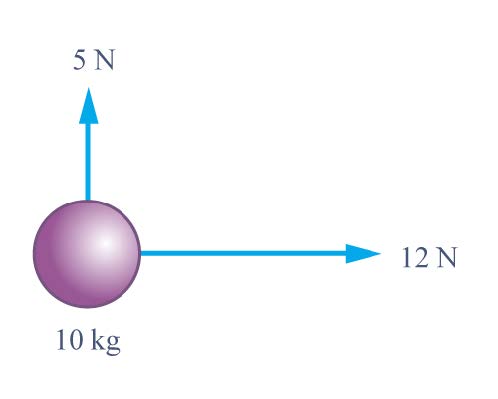
| 43. | แรง 5 นิวตัน และ 12 นิวตัน ในระนาบระดับมีทิศตั้งฉากกัน กระทำต่อมวล 10 กิโลกรัม บนพื้นระดับลื่นจงหาขนาดของความเร่งของมวลนี้
 |
| 44. | วัตถุมวล 20 กิโลกรัม มีแรงลัพธ์มากระทำต่อมวล ทำให้มวลเคลื่อนที่โดยมีความเร็วสัมพันธ์กับเวลา ดังกราฟ จงหาแรงลัพธ์ที่กระทำ ต่อวัตถุ  |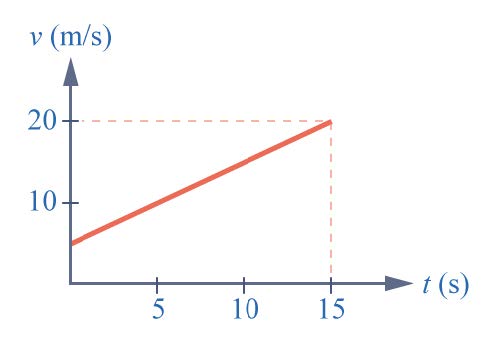
| 45. | กล่องมวล m ไถลลงพื้นเอียงซึ่งทำมุม θ กับแนวระดับด้วยความเร่ง a ต่อมาเพิ่มมวลให้กล่องเป็น 2m ความเร่งจะเป็นเท่าใด ถ้าสัมประสิทธิ์ของความเสียดทานระหว่างกล่องกับพื้นเอียงมีค่าคงที่ |
| 46. | ลิ่มวางอยู่บนพื้นฝืดมาก ผิวบนของลิ่มเป็นผิวราบลื่นนำมวล M มาวางและปล่อยให้ไถลลงบนผิวลื่นนี้แรงที่ลิ่มกดทับพื้นระดับจะเพิ่มขึ้นจากเดิมเท่าใด
 |
| 47. | ในการทดลองเพื่อพิสูจน์กฎการเคลื่อนที่ของนิวตัน มีการชดเชยความฝืดและใช้ขนาดต่างๆ ลากมวล (รถทดลอง) และวัดความเร่ง เมื่อเขียนกราฟระหว่างแรงและความเร่งได้กราฟ
 |
| 48. | ผูกเชือก (ด้ายเย็บผ้าที่เหนียวพอประมาณ) กับถุงทรายดังภาพ ในระหว่างการดึงถุงขึ้นอย่างช้าๆ ทำให้เชือกไม่ขาด กับการดึงถุงขึ้นอย่างรวดเร็วทำให้เชือกขาด เหตุใดจึงเป็นเช่นนั้น จงอธิบาย
 |
ตอบ
แรงที่กระทำต่อถุงทรายจะมี 2 แรงคือแรงดึงเชือก \(\rm \vec{T}\) และน้ำหนักวัตถุ \(\rm m\vec{g}\) พิจารณาเมื่อถุงทรายเคลื่อนที่ขึ้นอย่างช้าๆ ถือว่าถุงทรายมีความเร็วคงตัว แรงลัพธ์ที่กระทำต่อวัตถุเป็นศูนย์ จะได้ขนาดของแรงดึงขึ้นมีค่าเท่ากับขนาดของแรงดึงลง นั้นคือ \(\rm T=mg\)
พิจารณาเมื่อดึงถุงทรายอย่างรวดเร็ว ถุงทรายจะเคลื่อนที่ด้วยความเร่ง
จากกฎการเคลื่อนที่ข้อที่สองของนิวตัน
จะได้
แรงที่กระทำต่อถุงทรายจะมี 2 แรงคือแรงดึงเชือก \(\rm \vec{T}\) และน้ำหนักวัตถุ \(\rm m\vec{g}\) พิจารณาเมื่อถุงทรายเคลื่อนที่ขึ้นอย่างช้าๆ ถือว่าถุงทรายมีความเร็วคงตัว แรงลัพธ์ที่กระทำต่อวัตถุเป็นศูนย์ จะได้ขนาดของแรงดึงขึ้นมีค่าเท่ากับขนาดของแรงดึงลง นั้นคือ \(\rm T=mg\)
พิจารณาเมื่อดึงถุงทรายอย่างรวดเร็ว ถุงทรายจะเคลื่อนที่ด้วยความเร่ง
จากกฎการเคลื่อนที่ข้อที่สองของนิวตัน
\(\rm Σ\vec{F} = m\vec{a}\)
ให้ทิศขึ้นแทนด้วยเครื่องหมาย + และทิศลงแทนด้วยเครื่องหมาย -จะได้
\(\rm T=ma+mg\)
จะเห็นว่า \(\rm T > mg\) เมื่อดึงถุงทรายอย่างรวดเร็วเชือกจะขาด เพราะแรงดึงเชือกมากเกินค่าแรงที่เส้นเชือกรับได้สูงสุด| 49. | สปริงเบาทั้งสามอันเหมือนกันหมด ถ้าสปริงในรูป ก. ยืดออก 4 เซนติเมตร สปริงในรูป ข. ยืดออกรวมเป็นกี่เซนติเมตรเมื่อแขวนมวลขนาดเท่ากันกับรูป ก.
 |
| 50. | มวล 1.0 กิโลกรัมสองก้อน ผูกติดกับเชือกเบาและแขวนติดกับเพดานของลิฟต์ดังรูป ถ้าลิฟต์เคลื่อนที่ลงด้วยความเร่ง 2 m/s2 จงหาแรงตึงในเส้นเชือก T1 และ T2
 |
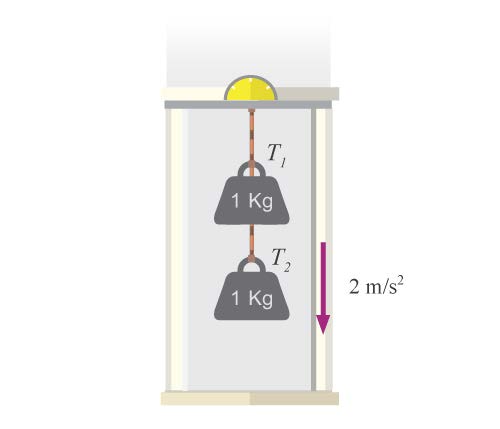| 51. | เข็มขัดนิรภัยและที่พิงศีรษะซึ่งติดอยู่กับเบาะในรถยนต์มีไว้เพื่อประโยชน์อะไร จงอธิบายพร้อมเหตุผล |
ตอบ เมื่อรถถูกชนจากด้านหลัง ที่พิงศีรษะสามารถป้องกันไม่ให้ศีรษะเคลื่อนที่ไปด้านหลังมากเกินไปทำให้คอไม่หัก เมื่อถูกชนจากด้านหน้าเข็มขัดนิรภัยจะช่วยไม่ให้ลำตัวกระแทกกับพวงมาลัย
| 52. | จากรูป กล่อง A และ B มีมวล 20 และ 10 กิโลกรัม ดึงวัตถุ A ด้วยแรงขนาน 200 นิวตัน ถ้าสัมประสิทธิ์ของความเสียดทานระหว่าง A กับพื้นและกล่อง A กับกล่อง B เป็น 0.4 และ 0.2 ตามลำดับ จงหาความเร่งของกล่อง A
 |
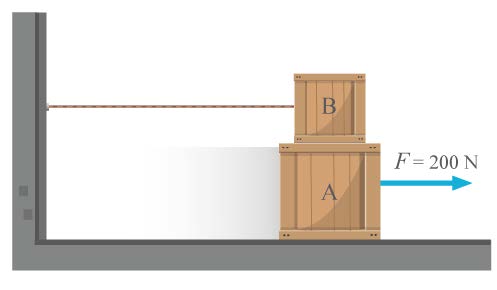| 53. | แรงเสียดทานมีผลต่อการเดินเช่นไร จงใหเ้หตุผลประกอบ |
| 54. | จากการทดลองเรื่องสัมประสิทธิ์ความเสียดทาน เมื่อจัดรางไม่ให้พื้นรางอยู่ในแนวระดับ และใช้เครื่องชั่งสปริงเกี่ยวขอของแผ่นไม้ที่มีถุงทรายทับอยู่บนแล้วออกแรง ดึงเครื่องชั่งสปริงให้ทิศของแรงดึงอยู่ในแนวระดับ ทำให้ได้ข้อมูลที่นำไปเขียนกราฟเพื่อแสดงความสัมพันธ์ระหว่างขนาดแรงดึง (F) กับน้ำหนักถุงทรายรวมกับขนาดของน้ำหนักแผ่นไม้ (W) ได้กราฟดังรูป จงหาสัมประสิทธิ์ความเสียดทาน
 |
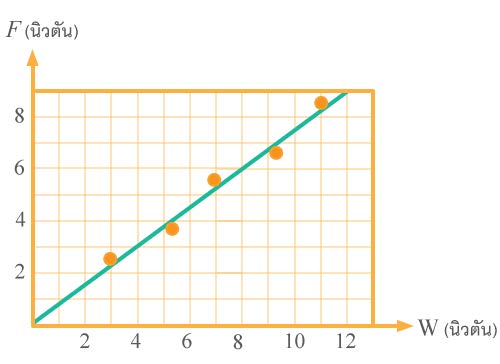| 55. | กล่องสองใบมวล m1 และ m2 ตามลำดับ วางซ้อนกันบนพื้นราบไร้ความฝืด มีแรง F กระทำต่อกล่อง ทำให้กล่องทั้งสองเคลื่อนที่ไปทางขวาด้วยความเร่ง a ถ้า f เป็นแรงเสียดทานสูงสุดที่มีได้ระหว่างผิวสัมผัสของกล่องทั้งสอง F มีค่าได้มากที่สุดเท่าใด มวล m2 จึงไม่ไถลบน m1
 |
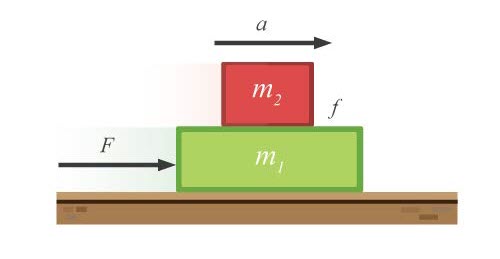