หัวข้อฟิสิกส์ : การอนุรักษ์พลังงาน
| 1. | ให้คานบางสม่ำเสมอ มวล m ยาว L อยู่ภายใต้แรงโน้มถ่วง g โมเมนต์ความเฉื่อยในการหมุนของคานรอบจุดศูนย์กลางเท่ากับ md2 แล้วอัตราส่วน L/d เท่ากับข้อใด |
| A | \(3\sqrt2\) |
| B | \(3\) |
| C | \(12\) |
| D | \(2\sqrt3\) |
| E | ไม่มีข้อใดถูก |
ตอบ (D)
พิจารณาความเฉื่อยในการหมุนรอบจุดศูนย์กลางของคานบางสม่ำเสมอ จะได้
พิจารณาความเฉื่อยในการหมุนรอบจุดศูนย์กลางของคานบางสม่ำเสมอ จะได้
\({{\rm{I}}_{{\rm{cm}}}}{\rm{ = }}\dfrac{{\rm{1}}}{{{\rm{12}}}}{\rm{m}}{{\rm{L}}^{\rm{2}}}\)
จากโจทย์ให้ความเฉื่อยในการหมุนของคานรอบจุดศูนย์กลางเท่ากับ md2 เมื่อแทนที่ Icm จะได้
\(\begin{align*}{\rm{m}}{{\rm{d}}^{\rm{2}}} &= \dfrac{{\rm{1}}}{{{\rm{12}}}}{\rm{m}}{{\rm{L}}^{\rm{2}}}\\ {{\rm{L}}^{\rm{2}}} &= {\rm{12}}{{\rm{d}}^{\rm{2}}}\\ \dfrac{{\rm{L}}}{{\rm{d}}} &= \sqrt {12} \end{align*}\)
ดังนั้น \(\rm L/d = 2\sqrt3\)| 2. | ให้คานบางสม่ำเสมอ มวล m ยาว L อยู่ภายใต้แรงโน้มถ่วง g โมเมนต์ความเฉื่อยในการหมุนของคานรอบจุดศูนย์กลางเท่ากับ md2 ถ้าคานถูกแขวน ณ ตำแหน่งที่ห่างจากจุดศูนย์กลางไป kd และถูกสั่นเบาๆ ด้วยความถี่เชิงมุม β\(\sqrt{ \rm \dfrac{g}{d}}\) แล้วค่าของ β ในเทอมของ k เท่ากับข้อใด |
| A | \(\rm 1+k^2\) |
| B | \(\rm \sqrt{1+k^2}\) |
| C | \(\rm \sqrt{\dfrac{k}{1+k}}\) |
| D | \(\rm \sqrt{\dfrac{k^2}{1+k}}\) |
| E | ไม่มีข้อใดถูก |
ตอบ (E)
จากที่ทอร์กของแรงโน้มถ่วงจะเท่ากับมวลที่จุดศูนย์กลางมวล จะได้ว่า ทอร์กของแรงโน้มถ่วงที่กระทำกับแกนที่ผ่านจุดแขวนคานที่ห่างจากจุดศูนย์กลางไป kd ขณะคานทำมุม θ กับแนวตั้ง จะเท่ากับ
เมื่อมุมที่เกิดการสั่นนั้นเล็กมาก จะได้ว่า sin θ ≈ θ จึงได้
เนื่องจากวัตถุสั่นด้วยความถี่เชิงมุม ω ดังนั้น การเคลื่อนที่ของวัตถุจะเป็นไปตามสมการเชิงอนุพันธ์
เราจะได้
ดังนั้น \(\beta = \sqrt {\dfrac{{\rm{k}}}{{{\rm{(1 + }}{{\rm{k}}^{\rm{2}}}{\rm{)}}}}} \)
จากที่ทอร์กของแรงโน้มถ่วงจะเท่ากับมวลที่จุดศูนย์กลางมวล จะได้ว่า ทอร์กของแรงโน้มถ่วงที่กระทำกับแกนที่ผ่านจุดแขวนคานที่ห่างจากจุดศูนย์กลางไป kd ขณะคานทำมุม θ กับแนวตั้ง จะเท่ากับ
\({\tau _{\rm{p}}}=\rm - mg~k~d ~sin \theta\) --- (1)
ให้ p ที่ห้อยอยู่หมายถึง จุดหมุน จากนั้นเราจะใช้ทฤษฎีบทของแกนขนานหาความเฉื่อยในการหมุนรอบจุดหมุน จะได้ว่า\(\rm I_p = I_{cm} + mh^2 = md^2 + m (kd)^2\)
\(\rm I_p = md^2 (1+k^2) \) --- (2)
จากนั้นใช้กฎข้อที่สองของนิวตันหาการหมุนของแกนที่ผ่านจุดหมุน สังเกตว่าแรงที่จุดหมุนไม่ได้ทำให้เกิดทอร์กกับแกนที่ผ่านจุดหมุนเลย เมื่อใช้สมการที่ (1) และ (2) จะได้ว่า
\(\begin{align*} {\tau _{\rm{p}}} &=\rm I{{\rm{ }}_{\rm{p}}}{\rm{\alpha }}\\ \rm - mg~k~d ~sin \theta &= \rm m{{\rm{d}}^{\rm{2}}}\left( {{\rm{1 + }}{{\rm{k}}^{\rm{2}}}} \right)\frac{{{{\rm{d}}^{\rm{2}}}{\rm{\theta }}}}{{{\rm{d}}{{\rm{t}}^{\rm{2}}}}} \end{align*}\)
เมื่อมุมที่เกิดการสั่นนั้นเล็กมาก จะได้ว่า sin θ ≈ θ จึงได้
\(\dfrac{{{{\rm{d}}^2}{\rm{\theta }}}}{{{\rm{d}}{{\rm{t}}^2}}} = - \dfrac{{{\rm{gk}}}}{{{\rm{d(1 + }}{{\rm{k}}^{\rm{2}}}{\rm{)}}}}{\rm{\theta }}\)
เนื่องจากวัตถุสั่นด้วยความถี่เชิงมุม ω ดังนั้น การเคลื่อนที่ของวัตถุจะเป็นไปตามสมการเชิงอนุพันธ์
\(\dfrac{{{{\rm{d}}^2}{\rm{\theta }}}}{{{\rm{d}}{{\rm{t}}^2}}} = - {{\rm{\omega }}^2}{\rm{\theta }}\)
เราจะได้
\({\rm{\omega = }}\sqrt {\dfrac{{{\rm{gk}}}}{{{\rm{d(1 + }}{{\rm{k}}^{\rm{2}}}{\rm{)}}}}} = \sqrt {\dfrac{{\rm{k}}}{{{\rm{(1 + }}{{\rm{k}}^{\rm{2}}}{\rm{)}}}}} \sqrt {\dfrac{{\rm{g}}}{{\rm{d}}}} \)
จากโจทย์ให้ \({\rm{\omega }} = \beta \sqrt {\dfrac{{\rm{g}}}{{\rm{d}}}}\)ดังนั้น \(\beta = \sqrt {\dfrac{{\rm{k}}}{{{\rm{(1 + }}{{\rm{k}}^{\rm{2}}}{\rm{)}}}}} \)
| 3. | (เกินหลักสูตรการสอบเข้า สอวน. 1) ให้คานบางสม่ำเสมอ มวล m ยาว L อยู่ภายใต้แรงโน้มถ่วง g โมเมนต์ความเฉื่อยในการหมุนของคานรอบจุดศูนย์กลางเท่ากับ md2 ถ้าคานถูกแขวน ณ ตำแหน่งที่ห่างจากจุดศูนย์กลางไป kd และถูกสั่นเบาๆ ด้วยความถี่เชิงมุม β\(\sqrt{ \rm \dfrac{g}{d}}\) ค่าของ β สูงสุด จะเท่ากับข้อใด |
| A | \(1\) |
| B | \(\sqrt2\) |
| C | \(1/\sqrt2\) |
| D | ไม่สามารถหาค่า β สูงสุดได้ |
| E | ไม่มีข้อใดถูก |
ตอบ (C)
จากที่ทอร์กของแรงโน้มถ่วงจะเท่ากับมวลที่จุดศูนย์กลางมวล จะได้ว่า ทอร์กของแรงโน้มถ่วงที่กระทำกับแกนที่ผ่านจุดแขวนคานที่ห่างจากจุดศูนย์กลางไป kd ขณะคานทำมุม θ กับแนวตั้ง จะเท่ากับ
เมื่อมุมที่เกิดการสั่นนั้นเล็กมาก จะได้ว่า sin θ ≈ θ จึงได้
เนื่องจากวัตถุสั่นด้วยความถี่เชิงมุม ω ดังนั้น การเคลื่อนที่ของวัตถุจะเป็นไปตามสมการเชิงอนุพันธ์
เราจะได้
เราจะต้องหาค่า k ที่ทำให้ β มีค่าสูงสุด โดยการหาอนุพันธ์เทียบ k ทั้งสองข้างจะได้
สังเกตว่า \(\dfrac{{{\rm{d\beta }}}}{{{\rm{dk}}}}{\rm{ = 0}}\) เมื่อ k = 1
แทน k = 1 ใน \({\rm{\beta = }}\sqrt {\dfrac{{\rm{k}}}{{{\rm{1 + }}{{\rm{k}}^{\rm{2}}}}}} \) จะได้ \({\rm{\beta = }}\sqrt {\dfrac{{\rm{1}}}{{\rm{2}}}} \)
จากที่ทอร์กของแรงโน้มถ่วงจะเท่ากับมวลที่จุดศูนย์กลางมวล จะได้ว่า ทอร์กของแรงโน้มถ่วงที่กระทำกับแกนที่ผ่านจุดแขวนคานที่ห่างจากจุดศูนย์กลางไป kd ขณะคานทำมุม θ กับแนวตั้ง จะเท่ากับ
\({\tau _{\rm{p}}}=\rm - mg~k~d ~sin \theta\) --- (1)
ให้ p ที่ห้อยอยู่หมายถึง จุดหมุน จากนั้นเราจะใช้ทฤษฎีบทของแกนขนานหาความเฉื่อยในการหมุนรอบจุดหมุน จะได้ว่า\(\rm I_p = I_{cm} + mh^2 = md^2 + m (kd)^2\)
\(\rm I_p = md^2 (1+k^2) \) --- (2)
จากนั้นใช้กฎข้อที่สองของนิวตันหาการหมุนของแกนที่ผ่านจุดหมุน สังเกตว่าแรงที่จุดหมุนไม่ได้ทำให้เกิดทอร์กกับแกนที่ผ่านจุดหมุนเลย เมื่อใช้สมการที่ (1) และ (2) จะได้ว่า
\(\begin{align*} {\tau _{\rm{p}}} &=\rm I{{\rm{ }}_{\rm{p}}}{\rm{\alpha }}\\ \rm - mg~k~d ~sin \theta &= \rm m{{\rm{d}}^{\rm{2}}}\left( {{\rm{1 + }}{{\rm{k}}^{\rm{2}}}} \right)\frac{{{{\rm{d}}^{\rm{2}}}{\rm{\theta }}}}{{{\rm{d}}{{\rm{t}}^{\rm{2}}}}} \end{align*}\)
เมื่อมุมที่เกิดการสั่นนั้นเล็กมาก จะได้ว่า sin θ ≈ θ จึงได้
\(\dfrac{{{{\rm{d}}^2}{\rm{\theta }}}}{{{\rm{d}}{{\rm{t}}^2}}} = - \dfrac{{{\rm{gk}}}}{{{\rm{d(1 + }}{{\rm{k}}^{\rm{2}}}{\rm{)}}}}{\rm{\theta }}\)
เนื่องจากวัตถุสั่นด้วยความถี่เชิงมุม ω ดังนั้น การเคลื่อนที่ของวัตถุจะเป็นไปตามสมการเชิงอนุพันธ์
\(\dfrac{{{{\rm{d}}^2}{\rm{\theta }}}}{{{\rm{d}}{{\rm{t}}^2}}} = - {{\rm{\omega }}^2}{\rm{\theta }}\)
เราจะได้
\({\rm{\omega = }}\sqrt {\dfrac{{{\rm{gk}}}}{{{\rm{d(1 + }}{{\rm{k}}^{\rm{2}}}{\rm{)}}}}} = \sqrt {\dfrac{{\rm{k}}}{{{\rm{(1 + }}{{\rm{k}}^{\rm{2}}}{\rm{)}}}}} \sqrt {\dfrac{{\rm{g}}}{{\rm{d}}}} \)
จากโจทย์ให้ \({\rm{\omega }} = \beta \sqrt {\dfrac{{\rm{g}}}{{\rm{d}}}}\) ดังนั้น \(\beta = \sqrt {\dfrac{{\rm{k}}}{{{\rm{(1 + }}{{\rm{k}}^{\rm{2}}}{\rm{)}}}}} \)เราจะต้องหาค่า k ที่ทำให้ β มีค่าสูงสุด โดยการหาอนุพันธ์เทียบ k ทั้งสองข้างจะได้
\({\rm{2\beta }}\dfrac{{{\rm{d\beta }}}}{{{\rm{dk}}}}{\rm{ = }}\dfrac{{{\rm{(1 + }}{{\rm{k}}^{\rm{2}}}{\rm{)}} - {\rm{k(2k)}}}}{{{{{\rm{(1 + }}{{\rm{k}}^{\rm{2}}}{\rm{)}}}^{\rm{2}}}}}{\rm{ = }}\dfrac{{{\rm{1}} - {{\rm{k}}^{\rm{2}}}}}{{{{{\rm{(1 + }}{{\rm{k}}^{\rm{2}}}{\rm{)}}}^{\rm{2}}}}}\)
สังเกตว่า \(\dfrac{{{\rm{d\beta }}}}{{{\rm{dk}}}}{\rm{ = 0}}\) เมื่อ k = 1
แทน k = 1 ใน \({\rm{\beta = }}\sqrt {\dfrac{{\rm{k}}}{{{\rm{1 + }}{{\rm{k}}^{\rm{2}}}}}} \) จะได้ \({\rm{\beta = }}\sqrt {\dfrac{{\rm{1}}}{{\rm{2}}}} \)
| 4. | วัตถุมวล m ผูกติดกับทรงกระบอก รัศมี R ด้วยเชือกเบา ที่เวลา t = 0 วัตถุมีความเร็วต้น v0 ในทิศตั้งฉากกับเชือกที่มีความยาวเชือก L0 และแรงตึงในเส้นเชือกไม่เท่ากับศูนย์ ให้ทุกการเคลื่อนที่เกิดขึ้นบนพื้นที่ไม่มีแรงเสียดทานในแนวนอน ทรงกระบอกยังคงนิ่งอยู่บนพื้นและไม่มีการหมุน โดยวัตถุจะเคลื่อนหมุนวนไปรอบ ๆ ทรงกระบอก ซึ่งเชือกจะขาดเมื่อแรงตึงเชือกเกิน Tmax จงตอบคำถามในรูปของ Tmax , m, L0 , R , และ v0  |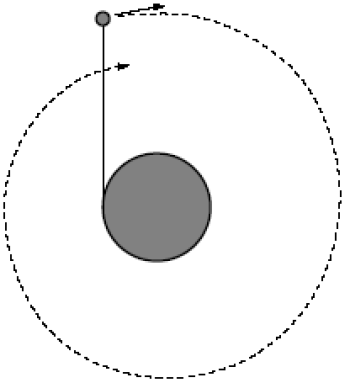
| A | \(\rm mv_0R\) |
| B | \(\rm \dfrac{m^2v_0^3}{T_{max}}\) |
| C | \(\rm mv_0L_0\) |
| D | \(\rm \dfrac{T_{max}R^2}{v_0}\) |
| E | ไม่มีข้อใดถูก |
ตอบ (B)
เนื่องจากทิศของความเร็วตั้งฉากกับเชือก จึงไม่เกิดงานที่เชือกกระทำกับวัตถุ และวัตถุเคลื่อนที่ขนานไปพื้นผิวทรงกระบอกที่ไม่มีแรงเสียดทาน ดังนั้น งานสุทธิที่กระทำกับวัตถุจะเท่ากับ ศูนย์ และทำให้การเปลี่ยนแปลงพลังงานจลน์ของวัตถุเป็นศูนย์
ดังนั้น พลังงานจลน์ของวัตถุขณะเชือกขาดจะเท่ากับพลังงานจลน์เริ่มต้นของวัตถุ
โดย r คือ รัศมีของวงแกว่งรอบทรงกระบอก (เชือกที่ยังไม่พันรอบทรงกระบอก)
ในวินาทีที่เชือกขาดจะเกิดแรงตึงสูงสุดเท่ากับ
เนื่องจากทิศของความเร็วตั้งฉากกับเชือก จึงไม่เกิดงานที่เชือกกระทำกับวัตถุ และวัตถุเคลื่อนที่ขนานไปพื้นผิวทรงกระบอกที่ไม่มีแรงเสียดทาน ดังนั้น งานสุทธิที่กระทำกับวัตถุจะเท่ากับ ศูนย์ และทำให้การเปลี่ยนแปลงพลังงานจลน์ของวัตถุเป็นศูนย์
ดังนั้น พลังงานจลน์ของวัตถุขณะเชือกขาดจะเท่ากับพลังงานจลน์เริ่มต้นของวัตถุ
\({\rm{K = }}\dfrac{{{\rm{mv}}_{\rm{0}}^{\rm{2}}}}{{\rm{2}}}\)
ดังนั้น อัตราเร็วของวัตถุจะเท่ากับ v0 เสมอ และโมเมนตัมเชิงมุมของวัตถุที่กระทำกับแกนของทรงกระบอกจะเท่ากับ\(\rm L = mv_0r\) --- (1)
โดย r คือ รัศมีของวงแกว่งรอบทรงกระบอก (เชือกที่ยังไม่พันรอบทรงกระบอก)
ในวินาทีที่เชือกขาดจะเกิดแรงตึงสูงสุดเท่ากับ
\({{\rm{T}}_{{\rm{max}}}}{\rm{ = }}\dfrac{{{\rm{mv}}_{\rm{0}}^{\rm{2}}}}{{\rm{r}}}\)
หรือ \({\rm{r = }}\dfrac{{{\rm{mv}}_{\rm{0}}^{\rm{2}}}}{{{{\rm{T}}_{{\rm{max}}}}}}\) เมื่อนำไปแทนใน (1) จะได้
\({\rm{L = }}\dfrac{{{{\rm{m}}^2}{\rm{v}}_{\rm{0}}^{\rm{3}}}}{{{{\rm{T}}_{{\rm{max}}}}}}\)
| 5. | วัตถุมวล m ผูกติดกับทรงกระบอก รัศมี R ด้วยเชือกเบา ที่เวลา t = 0 วัตถุมีความเร็วต้น v0 ในทิศตั้งฉากกับเชือกที่มีความยาวเชือก L0 และแรงตึงในเส้นเชือกไม่เท่ากับศูนย์ ให้ทุกการเคลื่อนที่เกิดขึ้นบนพื้นที่ไม่มีแรงเสียดทานในแนวนอน ทรงกระบอกยังคงนิ่งอยู่บนพื้นและไม่มีการหมุน โดยวัตถุจะเคลื่อนหมุนวนไปรอบ ๆ ทรงกระบอก ซึ่งเชือกจะขาดเมื่อแรงตึงเชือกเกิน Tmax จงตอบคำถามในรูปของ Tmax , m, L0 , R , และ v0  |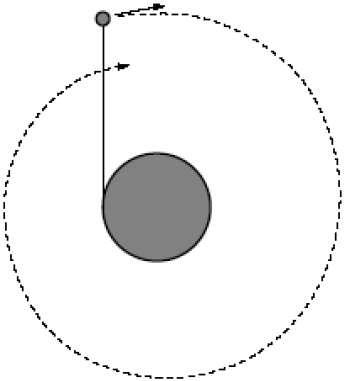
| A | \(\rm \dfrac{mv^2_0}{2}\) |
| B | \(\rm \dfrac{mv^2_0R}{2L_0}\) |
| C | \(\rm \dfrac{mv^2_0R^2}{2L^2_0}\) |
| D | \(\rm \dfrac{mv^2_0L_0^2}{2R^2}\) |
| E | ไม่มีข้อใดถูก |
ตอบ (A)
เนื่องจากทิศของความเร็วตั้งฉากกับเชือก จึงไม่เกิดงานที่เชือกกระทำกับวัตถุ และวัตถุเคลื่อนที่ขนานไปพื้นผิวทรงกระบอกที่ไม่มีแรงเสียดทาน ดังนั้น งานสุทธิที่กระทำกับวัตถุจะเท่ากับ ศูนย์ และทำให้การเปลี่ยนแปลงพลังงานจลน์ของวัตถุเป็นศูนย์
ดังนั้น พลังงานจลน์ของวัตถุขณะเชือกขาดจะเท่ากับพลังงานจลน์เริ่มต้นของวัตถุ จึงได้
เนื่องจากทิศของความเร็วตั้งฉากกับเชือก จึงไม่เกิดงานที่เชือกกระทำกับวัตถุ และวัตถุเคลื่อนที่ขนานไปพื้นผิวทรงกระบอกที่ไม่มีแรงเสียดทาน ดังนั้น งานสุทธิที่กระทำกับวัตถุจะเท่ากับ ศูนย์ และทำให้การเปลี่ยนแปลงพลังงานจลน์ของวัตถุเป็นศูนย์
ดังนั้น พลังงานจลน์ของวัตถุขณะเชือกขาดจะเท่ากับพลังงานจลน์เริ่มต้นของวัตถุ จึงได้
\({\rm{K = }}\dfrac{{{\rm{mv}}_{\rm{0}}^{\rm{2}}}}{{\rm{2}}}\)
| 6. | ให้เชือกเบาที่มีความยืดหยุ่นตามกฎของฮุค จะขาดเมื่อมีแรงตึง Tmax หากนำเชือกมาตรึงปลายด้านหนึ่งไว้ ส่วนปลายอีกด้านผูกกับมวล 3m และมวลที่สองขนาด m ซึ่งเล็กกว่า และมีอัตราเร็วต้น v0 พุ่งเข้าชนกับมวลแรก แล้วติดไปด้วยกัน จึงทำให้เชือกถูกดึงจนขาดออก โดยพลังงานจลน์สุดท้ายของมวลทั้งสองจะเท่ากับศูนย์ ถ้าการชนนั้นเกิดขึ้นในหนึ่งมิติ และยืดหยุ่นสมบูรณ์ แล้วขณะเชือกขาดมวลแรกจะหลุดออกไปด้วยอัตราเร็วสุดท้าย vf สมมุติให้ทุกการเคลื่อนที่เกิดขึ้นในแนวนอนและพื้นไม่มีแรงเสียดทาน แล้วค่า vf / v0 เท่ากับข้อใด |
| A | \(1/\sqrt{12}\) |
| B | \(1/\sqrt{2}\) |
| C | \(1/\sqrt{6}\) |
| D | \(1/\sqrt{3}\) |
| E | ไม่มีข้อใดถูก |
ตอบ (C)
โจทย์ให้เชือกขาดเมื่อถึงแรงตึงค่าหนึ่ง และเมื่อเชือกขาดก็จะเกิดพลังงานศักย์ U0 ขึ้น ในการชนที่ไม่ยืดหยุ่น (ขณะเชือกยังไม่ขาด) เราจะใช้กฎอนุรักษ์โมเมนตัม จึงได้ว่า
เนื่องจากทุกพลังงานศักย์ที่เกิดขึ้นจะถูกเปลี่ยนเป็นพลังงานจลน์ ทำให้ทราบว่าเชือกจะขาดเมื่อ
ต่อไปพิจารณา การชนแบบยืดหยุ่น เริ่มจากหาความเร็วต้นของมวลแต่ละอันหลังเกิดการชน (ขณะเชือกยังไม่ขาด)
วิธีที่ง่ายที่สุดคือหาจากจุดศูนย์กลางมวล จะได้
ในกรอบอ้างอิงนี้ ที่จุดศูนย์กลางมวลก่อนเกิดการชน m จะมีความเร็วเท่ากับ และ 3m มีความเร็วเท่ากับ \(\dfrac{{ - {{\rm{v}}_0}}}{4}\) สำหรับการชนแบบยืดหยุ่นในหนึ่งมิติ และจุดศูนย์กลางมวลแต่ละอันจะมีความเร็วหลังการชนเท่ากับก่อนชน แต่มีทิศทางตรงข้ามกับความเร็วก่อนชน ดังนั้น ความเร็วของ 3m หลังเกิดการชนจะไปทางขวาด้วย \(\dfrac{{ + {{\rm{v}}_0}}}{4}\)
เมื่อแปลง (2) กลับไปเราจะได้อัตราเร็วของ 3m หลังเกิดการชนเท่ากับ \(\dfrac{{ {{\rm{v}}_0}}}{2}\) และพลังงานจลน์หลังการชน (เชือกยังไม่ขาด) จะเท่ากับ
โจทย์ให้เชือกขาดเมื่อถึงแรงตึงค่าหนึ่ง และเมื่อเชือกขาดก็จะเกิดพลังงานศักย์ U0 ขึ้น ในการชนที่ไม่ยืดหยุ่น (ขณะเชือกยังไม่ขาด) เราจะใช้กฎอนุรักษ์โมเมนตัม จึงได้ว่า
\(\begin{align*} {\rm{m}}{{\rm{v}}_{\rm{0}}} &=\rm 4mv'\\ \rm v' &=\dfrac{{{{\rm{v}}_{\rm{0}}}}}{{\rm{4}}} \end{align*}\)
และพลังงานศักย์ของมวลทั้งสองหลังเกิดการชนจะเท่ากับ
\({{\rm{K}}_{\rm{1}}}{\rm{ = }}\dfrac{{{\rm{mv}}_{\rm{0}}^{\rm{2}}}}{{\rm{8}}}\)
เนื่องจากทุกพลังงานศักย์ที่เกิดขึ้นจะถูกเปลี่ยนเป็นพลังงานจลน์ ทำให้ทราบว่าเชือกจะขาดเมื่อ
\({{\rm{U}}_{\rm{0}}}{\rm{ = }}{{\rm{K}}_{\rm{1}}}{\rm{ = }}\dfrac{{{\rm{mv}}_{\rm{0}}^{\rm{2}}}}{{\rm{8}}}\) --- (1)
ต่อไปพิจารณา การชนแบบยืดหยุ่น เริ่มจากหาความเร็วต้นของมวลแต่ละอันหลังเกิดการชน (ขณะเชือกยังไม่ขาด)
วิธีที่ง่ายที่สุดคือหาจากจุดศูนย์กลางมวล จะได้
\({{\rm{v}}_{{\rm{cm}}}}{\rm{ = }}\dfrac{{{{\rm{v}}_0}}}{{\rm{4}}}\) --- (2)
ในกรอบอ้างอิงนี้ ที่จุดศูนย์กลางมวลก่อนเกิดการชน m จะมีความเร็วเท่ากับ และ 3m มีความเร็วเท่ากับ \(\dfrac{{ - {{\rm{v}}_0}}}{4}\) สำหรับการชนแบบยืดหยุ่นในหนึ่งมิติ และจุดศูนย์กลางมวลแต่ละอันจะมีความเร็วหลังการชนเท่ากับก่อนชน แต่มีทิศทางตรงข้ามกับความเร็วก่อนชน ดังนั้น ความเร็วของ 3m หลังเกิดการชนจะไปทางขวาด้วย \(\dfrac{{ + {{\rm{v}}_0}}}{4}\)
เมื่อแปลง (2) กลับไปเราจะได้อัตราเร็วของ 3m หลังเกิดการชนเท่ากับ \(\dfrac{{ {{\rm{v}}_0}}}{2}\) และพลังงานจลน์หลังการชน (เชือกยังไม่ขาด) จะเท่ากับ
\({{\rm{K}}_{\rm{2}}}{\rm{ = }}\dfrac{{{\rm{3mv}}_{\rm{0}}^{\rm{2}}}}{{\rm{8}}}\) --- (3)
แต่โจทย์กำหนดให้เชือกต้องขาด จากที่เราทราบว่า U0 ของพลังงานจนล์ของ 3m จะถูกส่งไปที่เชือก เราจะใช้กฎอนุรักษ์พลังงานร่วมกับสมการที่ (1) และ (3) จะได้
\({{\rm{K}}_{\rm{3}}}{\rm{ = }}{{\rm{K}}_{\rm{2}}} - {{\rm{K}}_{\rm{1}}}{\rm{ = }}\dfrac{{{\rm{3mv}}_{\rm{0}}^{\rm{2}}}}{{\rm{8}}} - \dfrac{{{\rm{3mv}}_{\rm{0}}^{\rm{2}}}}{{\rm{8}}}{\rm{ = }}\dfrac{{{\rm{mv}}_{\rm{0}}^{\rm{2}}}}{{\rm{4}}}\)
หาค่า vf / v0 จาก K3 ดังนี้
\(\begin{align*} {{\rm{K}}_{\rm{3}}}&= \dfrac{{{\rm{3mv}}_f^{\rm{2}}}}{{\rm{2}}} =\dfrac{{{\rm{mv}}_{\rm{0}}^{\rm{2}}}}{{\rm{4}}}\\ \frac{{{{\rm{v}}_{\rm{f}}}}}{{{{\rm{v}}_{\rm{0}}}}} &= \sqrt {\frac{1}{6}} \end{align*}\)
| 7. | ให้เชือกเบาที่มีความยืดหยุ่นตามกฎของฮุค จะขาดเมื่อมีแรงตึง Tmax หากนำเชือกมาตรึงปลายด้านหนึ่งไว้ ส่วนปลายอีกด้านผูกกับมวล 3m และมวลที่สองขนาด m ซึ่งเล็กกว่า และมีอัตราเร็วต้น v0 พุ่งเข้าชนกับมวลแรก แล้วติดไปด้วยกัน จึงทำให้เชือกถูกดึงจนขาดออก โดยพลังงานจลน์สุดท้ายของมวลทั้งสองจะเท่ากับศูนย์ ถ้าการชนนั้นเกิดขึ้นในหนึ่งมิติ และยืดหยุ่นสมบูรณ์ แล้วขณะเชือกขาดมวลแรกจะหลุดออกไปด้วยอัตราเร็วสุดท้าย vf สมมุติให้ทุกการเคลื่อนที่เกิดขึ้นในแนวนอนและพื้นไม่มีแรงเสียดทาน แล้วอัตราส่วนของพลังงานจลน์สุทธิของระบบของมวลทั้งสองหลังการชนแบบยืดยุ่นสมบูรณ์และเชือกได้ขาดออก กับ พลังงานจลน์เริ่มต้นของมวลที่สองก่อนเกิดการชน เท่ากับข้อใด |
| A | 1/4 |
| B | 1/3 |
| C | 1/2 |
| D | 3/4 |
| E | ไม่มีข้อใดถูก |
ตอบ (D)
พลังงานศักย์ของมวลทั้งสองหลังเกิดการชนเท่ากับ
และพลังงานจลน์หลังการชน (เชือกยังไม่ขาด) เท่ากับ
จากในกรอบอ้างอิง ที่จุดศูนย์กลางมวลหลังเกิดการชน m จะมีความเร็วเท่ากับ \(\dfrac{{ - 3{{\rm{v}}_0}}}{4}\) เมื่อแปลงกลับไปเราจะหาความเร็วของ m หลังชนกับมวลที่มี \(\dfrac{{{{\rm{v}}_0}}}{2}\) ได้ ดังนั้น พลังงานจลน์ของมวล m หลังเกิดการชนแบบยืดหยุ่นเท่ากับ
ใช้สมการ (1) และค่า K3 หาพลังงานจลน์รวมของระบบหลังเกิดการชนแบบยืดหยุ่นจะได้
ดังนั้น อัตราส่วนของพลังงานจลน์สุทธิของระบบหลังเกิดการชนแบบยืดหยุ่นกับพลังงานจลน์เริ่มต้นของมวล m ก่อนชนและทำให้เชือกขาดจะเท่ากับ
พลังงานศักย์ของมวลทั้งสองหลังเกิดการชนเท่ากับ
\({{\rm{K}}_{\rm{1}}} = \dfrac{{{\rm{mv}}_{\rm{0}}^{\rm{2}}}}{{\rm{8}}}\)
และพลังงานจลน์หลังการชน (เชือกยังไม่ขาด) เท่ากับ
\({{\rm{K}}_{\rm{2}}} = \dfrac{{{\rm{3mv}}_{\rm{0}}^{\rm{2}}}}{{\rm{8}}}\)
จากโจทย์กำหนดให้เชือกต้องขาด และเราทราบว่า U0 ของพลังงานจนล์ของ 3m จะถูกส่งไปที่เชือก เราจะใช้กฎอนุรักษ์พลังงานร่วมกับ K1 และ K2 จะได้
\({{\rm{K}}_{\rm{3}}}{\rm{ = }}{{\rm{K}}_{\rm{2}}} - {{\rm{K}}_{\rm{1}}}{\rm{ = }}\dfrac{{{\rm{3mv}}_{\rm{0}}^{\rm{2}}}}{{\rm{8}}} - \dfrac{{{\rm{3mv}}_{\rm{0}}^{\rm{2}}}}{{\rm{8}}}{\rm{ = }}\dfrac{{{\rm{mv}}_{\rm{0}}^{\rm{2}}}}{{\rm{4}}}\)
จากในกรอบอ้างอิง ที่จุดศูนย์กลางมวลหลังเกิดการชน m จะมีความเร็วเท่ากับ \(\dfrac{{ - 3{{\rm{v}}_0}}}{4}\) เมื่อแปลงกลับไปเราจะหาความเร็วของ m หลังชนกับมวลที่มี \(\dfrac{{{{\rm{v}}_0}}}{2}\) ได้ ดังนั้น พลังงานจลน์ของมวล m หลังเกิดการชนแบบยืดหยุ่นเท่ากับ
\({{\rm{K}}_{\rm{4}}}{\rm{ = }}\dfrac{{{\rm{mv}}_{\rm{0}}^{\rm{2}}}}{{\rm{8}}}\) --- (1)
ใช้สมการ (1) และค่า K3 หาพลังงานจลน์รวมของระบบหลังเกิดการชนแบบยืดหยุ่นจะได้
\({{\rm{K}}_4}{\rm{ + }}{{\rm{K}}_{\rm{3}}}{\rm{ = }}\dfrac{{{\rm{mv}}_{\rm{0}}^{\rm{2}}}}{8} + \dfrac{{{\rm{mv}}_{\rm{0}}^{\rm{2}}}}{{\rm{4}}} = \dfrac{{{\rm{3mv}}_{\rm{0}}^{\rm{2}}}}{8}\)
ดังนั้น อัตราส่วนของพลังงานจลน์สุทธิของระบบหลังเกิดการชนแบบยืดหยุ่นกับพลังงานจลน์เริ่มต้นของมวล m ก่อนชนและทำให้เชือกขาดจะเท่ากับ
\(\dfrac{{\frac{{{\rm{3mv}}_{\rm{0}}^{\rm{2}}}}{8}}}{{\frac{{{\rm{mv}}_{\rm{0}}^{\rm{2}}}}{2}}} = \dfrac{3}{4}\)
| 8. | นกบินเป็นเส้นตรง โดยเริ่มต้นบินด้วยอัตราเร็ว 10 m/s แล้วเพิ่มอัตราเร็วอย่างสม่ำเสมอจนถึง 18 m/s ได้ระยะทางทั้งหมด 40 m ความเร่งของนกเท่ากับข้อใด |
| A | 0.1 m/s2 |
| B | 0.2 m/s2 |
| C | 2.0 m/s2 |
| D | 2.8 m/s2 |
| E | 5.6 m/s2 |
ตอบ (D)
ให้เวลาผ่านไป t จาก \({\rm{a = }}\dfrac{{{\rm{\Delta v}}}}{{{\rm{\Delta t}}}}\) จะได้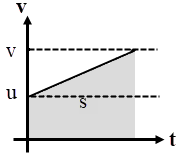
จาก s = พื้นที่สี่เหลี่ยมคางหมู
ให้เวลาผ่านไป t จาก \({\rm{a = }}\dfrac{{{\rm{\Delta v}}}}{{{\rm{\Delta t}}}}\) จะได้
\(\rm v – u = at\)
\(\rm t= \dfrac{{{\rm{v}} - {\rm{u}}}}{{\rm{a}}}\) --- (1)
จาก \({\rm{v = }}\dfrac{{{\rm{\Delta s}}}}{{{\rm{\Delta t}}}}\) ดังนั้น s เป็นพื้นที่ใต้กราฟ v – t
\(\rm s = \dfrac{1}{2}(v + u)t\)
จาก (1)
\(\begin{align*} {\rm{s}} &= \frac{1}{2}(v + u)(\frac{{v - u}}{{\rm{a}}})\\ a &= \frac{1}{2}\left( {\frac{{(v + u)(v - u)}}{{\rm{s}}}} \right) \end{align*}\)
แทนค่า
\(\begin{align*} a &= \frac{1}{2}\left( {\frac{{(18 + 10)(18 - 10)}}{{{\rm{40}}}}} \right)\\ &= \frac{1}{2}\left( {\frac{{8 \times 28}}{{{\rm{40}}}}} \right)\\ &= 2.8\,\,\,{\rm{m/}}{{\rm{s}}^{\rm{2}}} \end{align*}\)
| 9. | แมลงสาบไต่อยู่ภายในลูกบาศก์ที่มีความยาวด้าน 3 m ถ้าแมลงสาบเริ่มจากมุมซ้ายล่างที่ด้านหลังของลูกบาศก์ แล้วไต่มาถึงมุมบนขวาที่ด้านหน้าของลูกบาศก์ แล้วการกระจัดของแมลงสาบเท่ากับข้อใด |
| A | \(3\sqrt2 \rm ~m\) |
| B | \(3^3\sqrt2 \rm ~m\) |
| C | \(3\sqrt3 \rm ~m\) |
| D | \(\rm 3m\) |
| E | \(\rm 9m\) |
ตอบ (C)
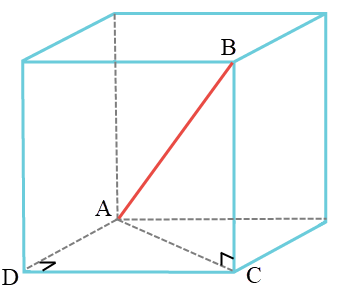สามเหลี่ยม ADC
\(\begin{align*} {\rm{A}}{{\rm{C}}^{\rm{2}}} &= \rm A{{\rm{D}}^{\rm{2}}}{\rm{ + D}}{{\rm{C}}^{\rm{2}}}\\ {\rm{A}}{{\rm{C}}^{\rm{2}}} &= {{\rm{3}}^{\rm{2}}}{\rm{ + }}{{\rm{3}}^{\rm{2}}}{\rm{ = 18 }}{{\rm{m}}^{\rm{2}}} \end{align*}\)
สามเหลี่ยม ABC
\(\begin{align*} {\rm{A}}{{\rm{B}}^{\rm{2}}} &= A{{\rm{C}}^{\rm{2}}}{\rm{ + B}}{{\rm{C}}^{\rm{2}}}\\ {\rm{A}}{{\rm{B}}^{\rm{2}}} &= 18 +{{\rm{3}}^{\rm{2}}}{\rm{ = 27 }}{{\rm{m}}^{\rm{2}}} \end{align*}\)
ดังนั้น \(\rm AB = 3\sqrt3 \rm ~m\)| 10. | ลูกตุ้มมวล m ยาว ℓ เริ่มแกว่งจากหยุดนิ่งในแนวระดับลงไปชนมวล M แล้วติดไปด้วยกัน หลังการชนมวล m จะแกว่งขึ้นไปได้ระยะทางสูงสุดเท่าใดจากพื้น (ข้อสอบคัดเลือก ม.4 ศูนย์เตรียม 26 ส.ค. 2555)  |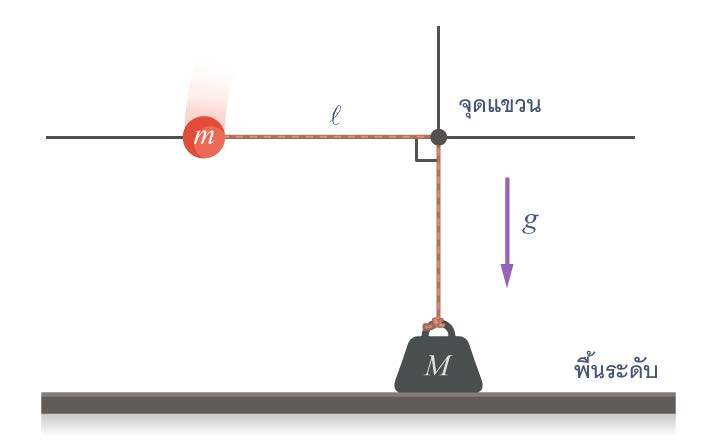
| 11. | มวล M ตั้งต้นเคลื่อนที่เข้าหากำแพงจากระยะห่าง D ด้วยความเร็วคงที่ v ที่จังหวะเดียวกันกับที่ลูกบอลเล็กๆ มวล m << M กระดอนจาก M แล้วด้วยความเร็ว u > v เทียบกับพื้นไปชนและกระดอนอย่างยืดหยุ่นจากกำแพงแข็งกลับมาชนกับ M อีก ที่จังหวะนี้ m ได้เคลื่อนที่ไปแล้วเป็นระยะทางรวมเท่าใดนับจากเมื่อชน M ครั้งแรก (ข้อสอบคัดเลือก ม.4 ศูนย์เตรียม 26 ส.ค. 2555)  |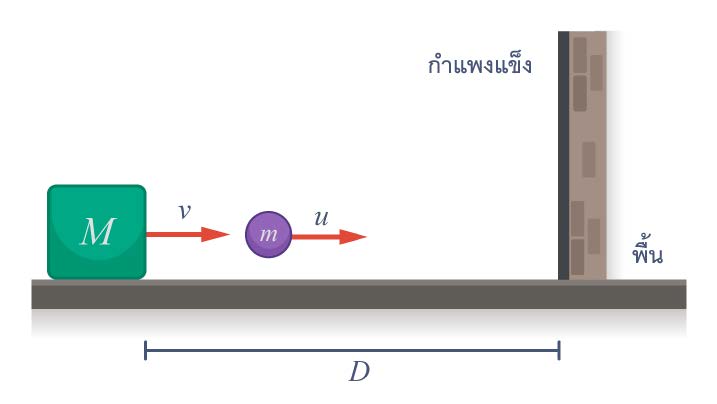
| 12. | สปริงมีความยาวธรรมชาติ ℓ ปลายหนึ่งยึดติดกำแพง อีกปลายหนึ่งยึดกับมวล m ถูกอัดไว้เป็นระยะทาง \(\dfrac{ℓ}{2}\) แล้วปล่อยให้ดันมวล m ไปชนมวล m เท่ากันอีกก้อนที่แค่เดิมอยู่นิ่งที่ B แล้วติดกันไป จะไปได้ไกลสุดเท่าใดจากจุด B (ข้อสอบคัดเลือก ม.5 ศูนย์เตรียม 3 ก.ย. 2549)  |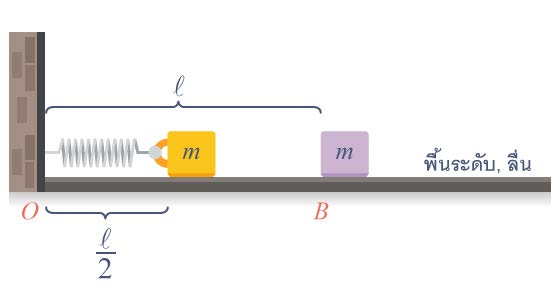
| 13. | จงแปลงค่าของพลังงานจลน์ \(\rm \dfrac{1}{2}mv^2=5\) จูล ไปอยู่ในหน่วยกรัม (มิลลิเมตรต่อวินาที)2 (ข้อสอบคัดเลือก ม.5 ศูนย์เตรียม 6 ก.ย. 2546) |
| 14. | มวล M อยู่นิ่งบนพื้นระดับลื่นและมีสปริงเบาติดอยู่ด้านซ้าย ค่าคงที่สปริงเท่ากับ k มวล m เคลื่อนที่ด้วยความเร็วต้น u เข้าชน สปริงจะหดเข้าไปมากที่สุดเป็นระยะทางเท่าไร (ข้อสอบคัดเลือก ม.5 ศูนย์เตรียม 6 ก.ย. 2546)  |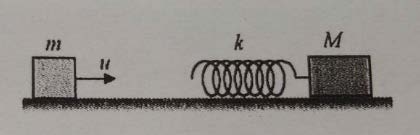
| 15. | โปรเจคไทล์ตั้งต้นจากจุด O เมื่อขึ้นไปถึงจุดสูงสุดก็ระเบิดออกเป็นสองชิ้นมวลเท่ากัน ชิ้นหน้าคือ A ชิ้นหลังคือ B ทันทีหลังระเบิด B มีความเร็วเป็นศูนย์เทียบกับพื้น ชิ้น A จะตกบนพื้นเลยจุดตกของ B ไปเป็นระยะทางกี่เท่าของระยะทาง OC (ข้อสอบคัดเลือก ม.4 ศูนย์เตรียม 26 ส.ค. 2555)  |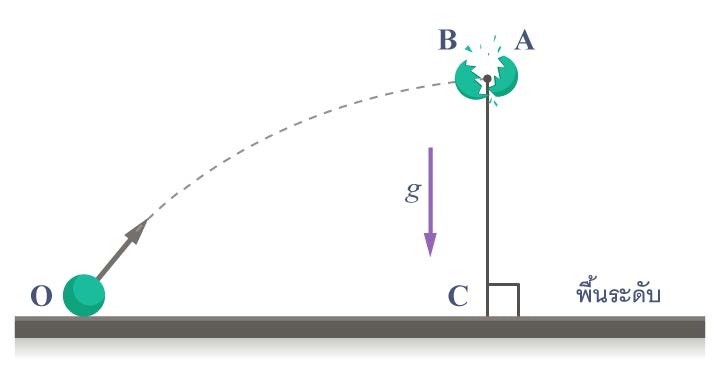
| 16. | ปล่อยลูกบอลมวล m จากจุดหยุดนิ่งจากที่สูง H จากพื้นทุกครั้งที่ลูกบอลกระทบพื้นจะกระดอนขึ้นด้วยอัตราเร็ว e(< 1) เท่าของอัตราเร็วก่อนกระทบพื้นพอดี ตอนที่ลูกบอลกระดอนขึ้นครั้งที่ n ลูกบอลมีพลังงานจลน์เท่าใด และจะกระดอนขึ้นไปได้สูงเท่าใดก่อนตกกลับลงมาอีก (ข้อสอบคัดเลือก ม.4 ศูนย์เตรียม 29 ส.ค. 2553) |
| 17. | ลูกปืนตะกั่วลูกหนึ่งเคลื่อนที่ด้วยอัตราเร็ว 200 m/s เข้าใส่เป้าและหยุดนิ่งอยู่ในเป้า สมมุติว่าพลังงานจลน์ทั้งหมดของลูกปืนเปลี่ยนเป็นความร้อนหมด และความร้อนนี้แบ่งไปให้ลูกปืนกับเป้าอย่างละเท่ากัน ลูกปืนมีอุณหภูมิเพิ่มขึ้นเท่าใด ความจุความร้อนจำเพาะของตะกั่วมีค่าเป็น 0.032 เท่าของน้ำ ความจุความร้อนจำเพาะของน้ำมีค่าเท่ากับ 1.00 cal/(g ⋅∘C) และ 1.00 cal มีค่าเท่ากับ 4.186 J (ข้อสอบคัดเลือก ม.4 ศูนย์เตรียม 30 ส.ค. 2552) |
| 18. | A กับ B เป็นมวลทรงกลมผิวเกลี้ยงรัศมีเท่ากัน A กำลังเคลื่อนที่ในแนว OX เข้าชน B ซึ่งอยู่นิ่งก่อนชนหลังการชนกันอย่างยืดหยุ่น แล้ว B จะกระเด็นทำมุมกี่องศากับแนว OX (ข้อสอบคัดเลือก ม.5 ศูนย์เตรียม 31 ส.ค. 2551)  |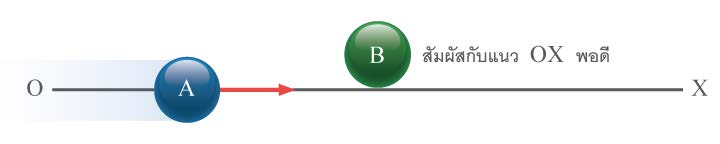
| 19. | ปล่อยมวลเล็ก ๆ ให้ไถลจากจุดหยุดนิ่งที่จุด A เข้าสู่รางวงกลม OB อย่างนุ่มนวล (ไม่มีการสะดุด, กระแทก) จะต้องให้จุด A อยู่สูงจากพื้นระดับเป็นกี่เท่าของรัศมีของราง OB จึงจะทำให้มวลนั้นขึ้นถึงจุด B ได้พอดีโดยไม่แยกตัวจากรางก่อน (ข้อสอบคัดเลือก ม.5 ศูนย์เตรียม 31 ส.ค. 2551)  |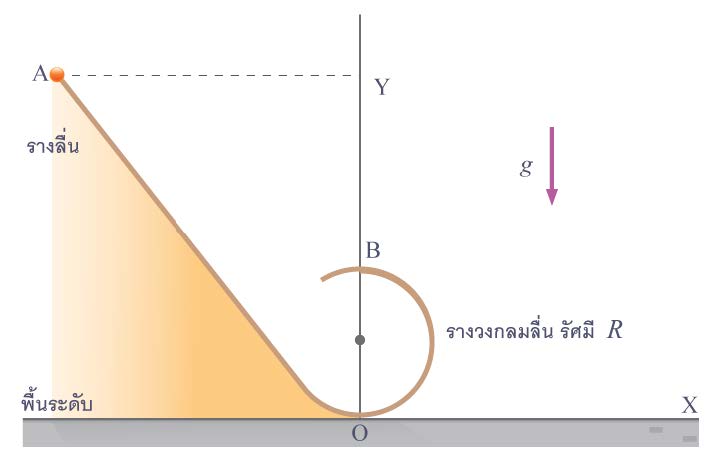
| 20. | ลูกบอลลูกหนึ่งตกลงมาจากที่สูง 10 m กระดอนกับพื้น และลอยกลับขึ้นไปได้สูง 2.5 m ถ้าลูกบอลกระทบพื้นนาน 0.10 s ความเร่งเฉลี่ยของลูกบอลระหว่างที่แตะพื้นมีขนาดเท่าใด (ข้อสอบคัดเลือก ม.4 ศูนย์เตรียม 31 ส.ค. 2551) |
| 21. | M กับ m ผูกโยงกันด้วยเส้นยางยืดหย่อนๆ อยู่บนผืนระดับรอบเเละลื่นต่อมาดีด M ไปทางขวาด้วยความเร็ว v∘ อึดใจต่อมาขณะที่เส้นยางยืดตึงที่สุดนั้น M มีความเร็วเป็นเท่าไรและพลังงานศักย์ของระบบขณะเดียวกันนั้นมีค่าเท่าไร (ข้อสอบคัดเลือก ม.5 ศูนย์เตรียม 1 ก.ย. 2556)  |
ตอบ \(\rm v_{_M} = \dfrac{M}{M +m}v_0\) และ \(\rm PE = \dfrac{1}{2}\left(\dfrac{mM}{M +m}\right) v^2_0\)
| 22. | ลูกตุ้ม M ห้อยอยู่นิ่ง ๆ มวล m เคลื่อนที่ด้วยความเร็ว u เข้าชนแล้วติดกันไปจะขึ้นไปได้สูงจากเดิมเป็นระยะทางเท่าไร (ข้อสอบคัดเลือก ม.4 ศูนย์เตรียม 31 ส.ค. 2557)  |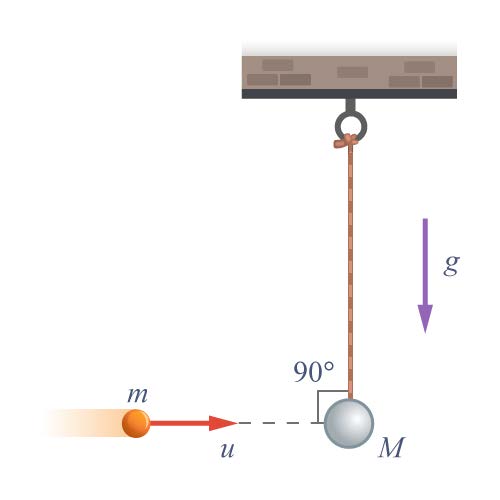
| 23. | มวล M รูปทรงกลมรัศมี R วางไว้ที่พื้นในห้องที่อุณหภูมิ t∘ จะมีพลังงานศักย์เพิ่มขึ้นหรือลดลงเท่าใด เมื่ออุณหภูมิห้องสูงขึ้นเป็น t1 (ข้อสอบคัดเลือก ม.4 ศูนย์เตรียม 12 ก.ย. 2547)  |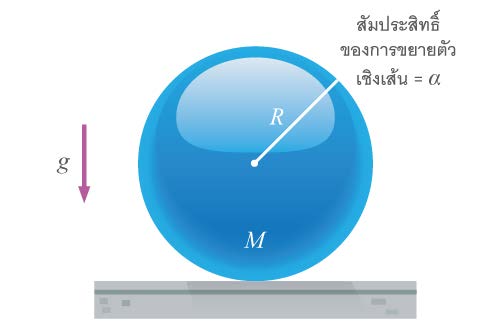
| 24. | มวล m1 กับ m2 ผูกติดกันด้วยเชือกยาว l และถูกเหวี่ยงให้หมุนอย่างอิสระบนโต๊ะระดับด้วยอัตราเร็วเชิงมุม ω ผู้สังเกตในระบบอ้างอิงเฉื่อยจะพบความเร็วสัมพันธ์ระหว่าง m2 กับ m1 มีขนาดเป็นเท่าใด (ข้อสอบคัดเลือก ม.5 ศูนย์เตรียม 3 ก.ย. 2549)  |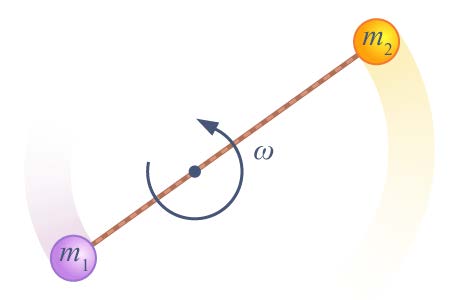
| 25. | จงตอบคำถามต่อไปนี้
1) จงพิสูจน์ว่าในกรอบอ้างอิงจุดศูนย์กลางมวลของระบบ โมเมนตัมของระบบมีค่ารวมกันเป็นศูนย์
2) จงแสดงว่าพลังงานจลน์ทั้งหมดของระบบมีค่าเท่ากับพลังงานจลน์ของจุดศูนย์กลางมวลของระบบบวกกับพลังงานจลน์รอบจุดศูนย์กลางมวลของระบบ
(ข้อสอบปลายค่าย 1 ม.4 ศูนย์เตรียม 24 ต.ค. 2552) |
ตอบ
1) จาก นิยามของ \(\rm v_{cm}\)จะได้
2) พลังงานจลน์ของระบบคือ
1) จาก นิยามของ \(\rm v_{cm}\)จะได้
\(\rm v_{cm}=\dfrac{\sum\limits_{i = 1}^{i = n} {m_iv_i} }{\sum\limits_{i = 1}^{i = n} {m_1}}\)
โมเมนตัมรวมของระบบเทียบจุดศูนย์กลางมวล คือ
\(\rm \sum\limits_{i = 1}^{i = n} {m_i{(v-v_{cm})}}i\)
จึงได้ว่า
\(\rm \sum\limits_{i = 1}^{i = n} {m_iv_i} - \sum\limits_{i = 1}^{i = n} {m_iv_{cm}} = 0\)
2) พลังงานจลน์ของระบบคือ
\(\rm \sum\limits_{i = 1}^{i = n} {\dfrac{1}{2}m_iv^2_i} = \sum\limits_{i = 1}^{i = n} {\dfrac{1}{2}m_i(v_{cm}+v_{i,cm})^2} = \sum\limits_{i = 1}^{i = n} {\dfrac{1}{2}m_iv^2_{cm}} + \sum\limits_{i = 1}^{i = n} {\dfrac{1}{2}m_iv^2_{i,cm}}\)
ใช้ผลจากข้อที่แล้วร่วมด้วย เพื่อตัดพจน์ตรงกลางทิ้งไป
\(\rm ∴ KE_{system} = KE_{cm} +KE_{around \,cm}\)
| 26. | 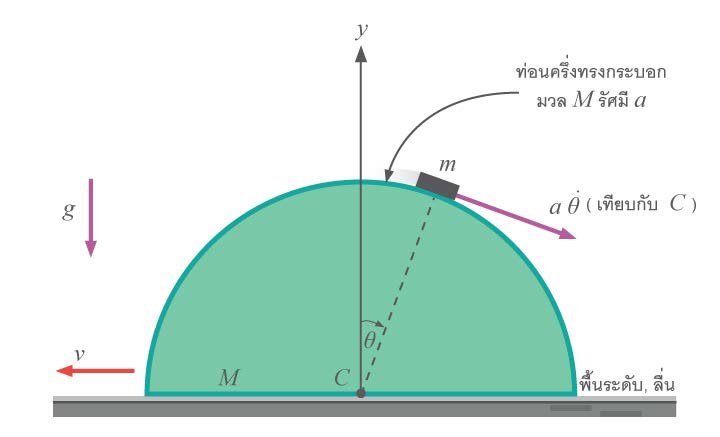 (ข้อสอบปลายค่าย 1 ม.5 ศูนย์เตรียม 25 ต.ค. 2551) |
ตอบ
1) \(\rm V=\dfrac{m\dotθRcos}{M+m}\)
2) \(\rm 2g(1-\cos\theta) = \left[\dfrac{M+m(1-\cos\theta)^2}{M+m}\right]a\dot\theta^2\)
3) \(\rm \theta=arccos\left[\dfrac{2(M+m)}{2(M+m)+M}\right]\)
1) \(\rm V=\dfrac{m\dotθRcos}{M+m}\)
2) \(\rm 2g(1-\cos\theta) = \left[\dfrac{M+m(1-\cos\theta)^2}{M+m}\right]a\dot\theta^2\)
3) \(\rm \theta=arccos\left[\dfrac{2(M+m)}{2(M+m)+M}\right]\)
| 27. | ออกแรงคงตัวขนาด 10 นิวตัน ลากกล่องใบหนึ่งให้เคลื่นอนที่ด้วยความเร็วคงตัวบนพื้นในแนวระดับที่มีความเสียดทาน จงหางานของแรงที่ลากกล่องและงานของแรงเสียดทานตามลำดับ ถ้าการกระจัดของกล่องเป็น 3 เมตร |
| 28. | หย่อนเชือกที่ผูกกับวัตถุให้เคลื่อนที่ลงเป็นระยะทาง S ด้วยความเร็วคงตัว งานของแรงที่เชือกดึงวัตถุเป็นเท่าใด |
| 29. | แรงที่สปริงทำกับมวลก้อนหนึ่งแสดงดังกราฟความสัมพันธ์ระหว่างแรงสปริงกับการกระจัดของมวลจากตำแหน่งสมดุล ดังรูป
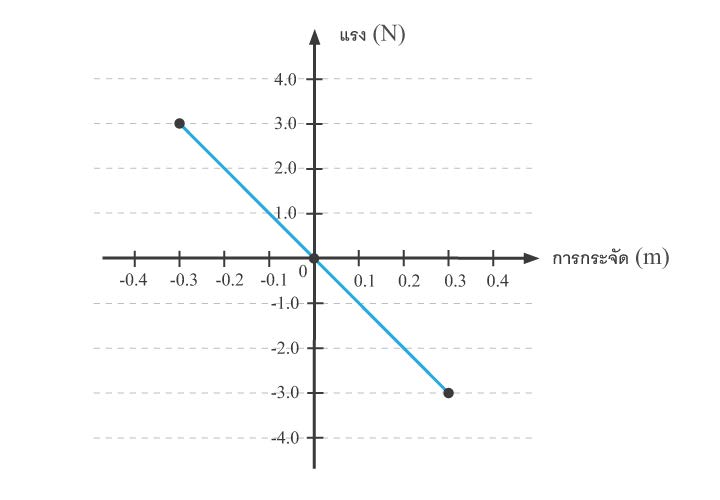 ข. งานของแรงสปริงในช่วงการกระจัดจาก -0.3 ถึง 0.3 เมตร |
| 30. | วัตถุมวล m อยสูู่งจากพื้นเป็นระยะทาง h พลังงานศักย์โน้มถ่วงของวัตถุนี้บนผิวโลกและบนผิวดวงจันทร์เท่ากันหรือไม่ |
| 31. | ถ้ามีแรงกระทำต่อวัตถุในทิศทางเดียวกับการเคลื่อนที่ของวัตถุ พลังงานจลน์ของวัตถุจะเปลี่ยนแปลงหรือไม่ อย่างไร ในทางกลับกันถ้าแรงนั้นมีทิศทางตรงข้าม พลังงานจลน์ของวัตถุจะเปลี่ยนแปลงหรือไม่ อย่างไร |
ตอบ เมื่อมีแรงกระทำต่อวัตถุในทิศทางเดียวกับการเคลื่อนที่ของวัตถุ จะทำให้วัตถุมีความเร็วเพิ่มขึ้น ดังนั้น พลังงานจลน์ของวัตถุจะเพิ่มขึน
ในทางกลับกัน ถ้าแรงที่กระทำต่อวัตถุมีทิศทางตรงข้าม จะทำให้วัตถุมีความเร็วลดลง ดังนั้น พลังงานจลน์ของวัตถุจะลดลง
ในทางกลับกัน ถ้าแรงที่กระทำต่อวัตถุมีทิศทางตรงข้าม จะทำให้วัตถุมีความเร็วลดลง ดังนั้น พลังงานจลน์ของวัตถุจะลดลง
| 32. | ปล่อยลูกกลมอันหนึ่งจากจุด X ตกสู่พื้นตามแนวดิ่งผ่านจุด Y ซึ่งเป็นจุดกึ่งกลางระหว่างตำแหน่ง X กับพื้นถ้าให้ Ep เป็นพลังงานศักย์โน้มถ่วงของวัตถุ และ Ek เป็นพลังงานจลน์ของวัตถุที่ตำแหน่ง Y จงหาความสัมพันธ์ของ Ep กับ Ek
 |
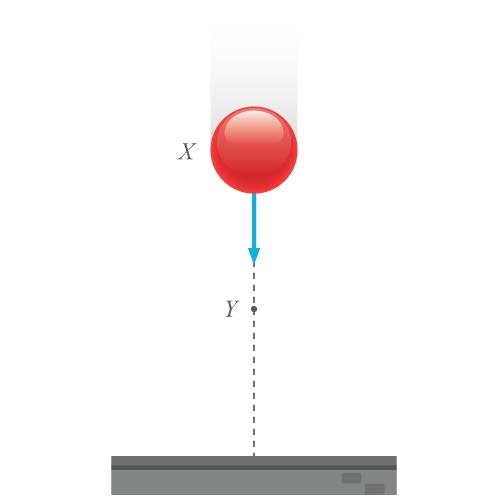| 33. | งานของแรง F ซึ่งกระทำกับวัตถุหนึ่งมีความสัมพันธ์กับระยะทางที่วัตถุเคลื่อนที่ S ดังรูป วัตถุใช้เวลาเคลื่อนที่ทั้งหมด 20 วินาที ในการทำงานของแรง F นี้กำลังเฉลี่ยของแรง F เป็นเท่าใด
 |
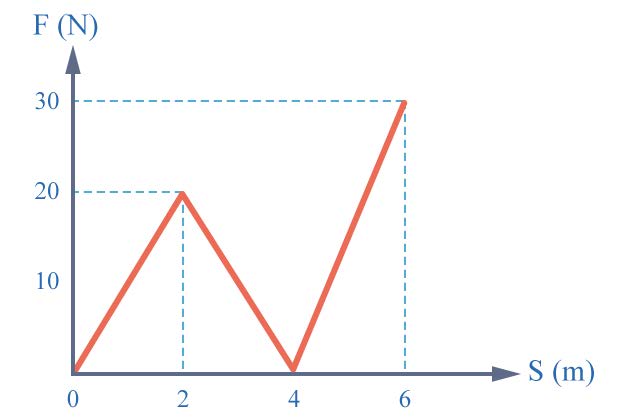| 34. | กรรมกรคนหนึ่งแบกของหนัก 50 กิโลกรัม ขึ้นไปบนภูเขา โดยเริ่มต้นที่จุด O แล้วเดินไปตามทาง OABC ถึงจุดหมายที่จุด C งานที่กรรมกรผู้นี้ทำจะเท่ากับ (ค่า g = 10 m/s2)
 |
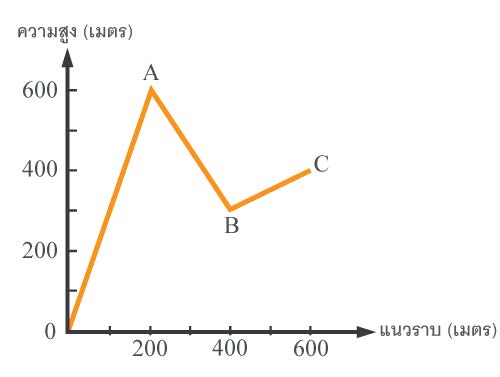| 35. | วัตถุมวล 1 กิโลกรัม เคลื่อนที่เป็นวงกลมอย่างสม่ำเสมอบนพื้นราบด้วยขนาดของความเร็ว 2 เมตรต่อวินาที โดยมีรัศมี 0.5 เมตร งานเนื่องจากแรงสู่ศูนย์กลางเมื่อวัตถุเคลื่อนที่ครึ่งรอบเป็นเท่าใด |
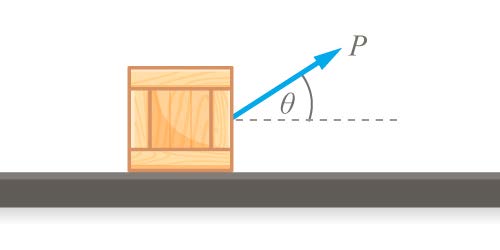
| 36. | กล่องหนัก 15 นิวตัน ถูกลากไปตามพื้นลื่นโดยแรง P = 30 นิวตัน ที่ทำมุม θ = 60∘ ด้วยความเร็ว 3 กิโลเมตรต่อชั่วโมง เป็นเวลา 1 นาที กำลังที่ใช้ในการลากกล่องเป็นเท่าไร
 |
| 37. | การเข็นรถไปตามพื้นราบและการเข็นรถไปตามพื้นเอียงด้วยอัตราเร็วคงตัวในระยะทางเท่ากัน กรณีใดต้องทำงานมากกว่ากันเพราะเหตุใด ถ้าถือว่าแรงเสียดทานที่กระทำต่อรถทั้งสองกรณีมีขนาดเท่ากัน |
ตอบ การเข็นรถไปตามพื้นเอียงต้องทำงานมากกว่าการเข็นรถไปตามพื้นราบ
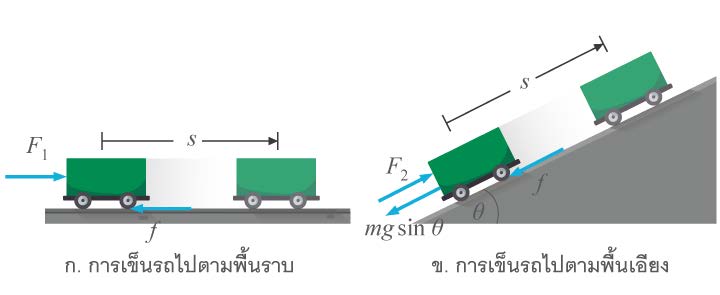
การเข็นรถไปตามพื้นราบ แรงที่กระทำต่อรถ และการกระจัด มีทิศทางเดียวกันงานของแรงที่กระทำต่อรถ คือ W1 = F1s
ดังรูป ก โดย
ดังรูป ก โดย
F1 = f
แต่การเข็น รถ (ขึ้น) ไปตามพื้นเอียง (ที่มีทิศทางทำมุม กับพื้นราบระดับ) แรงที่กระทำต่อรถ และการกระจัด งานของแรงที่กระทำต่อรถคือ W2 = F2s
ดังรูป ข โดย
ดังรูป ข โดย
F2 = mg sin θ + f
จะได ้F2 > F1 ดังนั้น W2 > W1
จึงสรุปได้ว่า การเข็นรถไปตามพื้นเอียงต้องทำงานมากกว่าการเข็นรถไปตามพื้นราบด้วยอัตรา เร็วคงตัวในระยะทางเท่ากันเมือแรงเสียดทานมีค่าเท่ากัน
จึงสรุปได้ว่า การเข็นรถไปตามพื้นเอียงต้องทำงานมากกว่าการเข็นรถไปตามพื้นราบด้วยอัตรา เร็วคงตัวในระยะทางเท่ากันเมือแรงเสียดทานมีค่าเท่ากัน
| 38. | ออกแรงคงที่ F ในแนวระดับดันกล่องใบหนึ่งให้เคลื่อนที่จากหยุดนึ่งไปบนพื้นระดับลื่น จงเขียนกราฟแสดงความสัมพันธ์ระหว่างกำลังขณะใด ๆ ของแรง F กับระยะทางที่วัตถุเคลื่อนที่ |
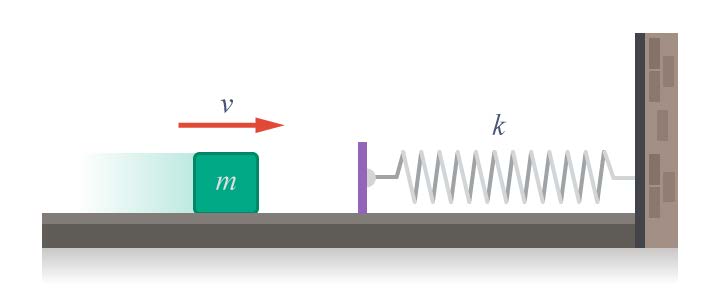
| 39. | มวล 2 กิโลกรัม เคลื่อนที่ในแนวราบบนพื้นที่มีแรงเสียดทาน 8 นิวตัน เข้าชนสปริงด้วยความเร็ว 2 เมตร/วินาที ทำให้สปริงหดได ้10 เซนติเมตร ค่าคงตัวของสปริงเป็นเท่าใดในหน่วยนิวตัน/เมตร
 |
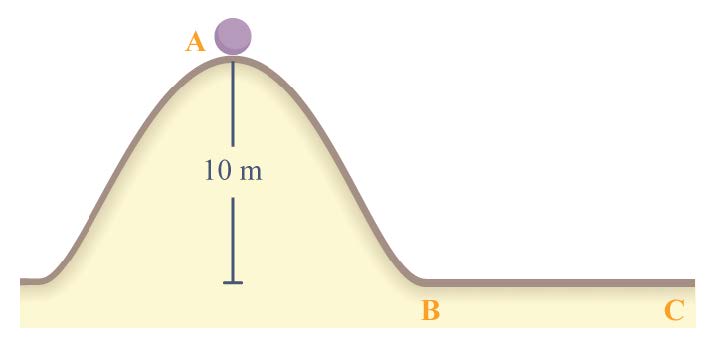
| 40. | จากรูป วัตถุเคลื่อนที่ลงจากทางโค้งซึ่งไม่มีแรงเสียดทาน เมื่อเคลื่อนที่ถึงพื้นราบ สัมประสิทธิ์ความเสียดทานระหว่างวัตถุกับพื้นราบเป็น 0.4 อยากทราบค่าวัตถุจะเคลื่นอนที่บนพื้นราบได้ไกลที่สุดเท่าไร
 |
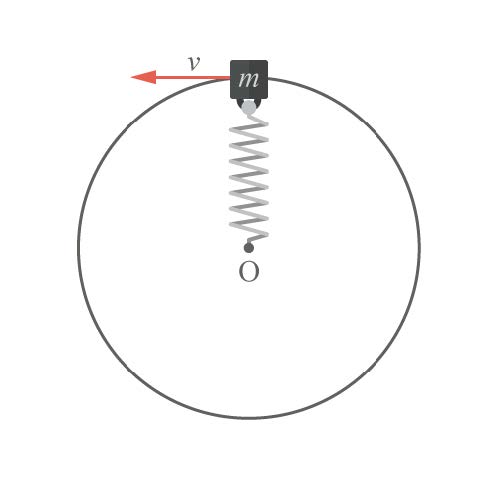
| 41. | ผูกมวล m ติดไว้ที่ปลายสปริงเบาซึ่งมีความยาวปกติ 40.0 เซนติเมตร และมีค่าคงตัวสปริงเท่ากับ 100 นิวตันต่อเมตร ถ้าเราแกว่งมวล m เป็นวงกลมบนพื้นโต๊ะลื่นรอบจุด O โดยมีรัศมีการเคลื่อนที่ 50.0 เซนติเมตร ขณะนั้นพลังงานจลน์ของมวลเป็นกี่เท่าของพลังงานศักย์ของสปริง
 |
