หัวข้อฟิสิกส์ : การแปลงหน่วย
| 1. | ให้การเคลื่อนที่ของวัตถุหนึ่งในสองมิติ เป็นไปตามสมการ
\(\rm \vec r(t) = (4.0t^2-9.0)\hat i + (2.0t - 5.0)\hat j \)
โดย r มีหน่วย เมตร และ t มีหน่วย วินาที แล้ววัตถุจะตัดแกน x ที่วินาทีใด |
| A | 0.0 s |
| B | 0.4 s |
| C | 0.6 s |
| D | 1.5 s |
| E | 2.5 s |
ตอบ (E)
จาก
จาก
\(\rm \vec r(t) = x(t)\hat i + y(t)\hat j \)
วัตถุตัดแกน x เมื่อ y(t) = 0
\(\begin{align*}\rm 2.0(t) -5.0 &= 0\\ \therefore \rm t &= 2.5 ~\rm s \end{align*}\)
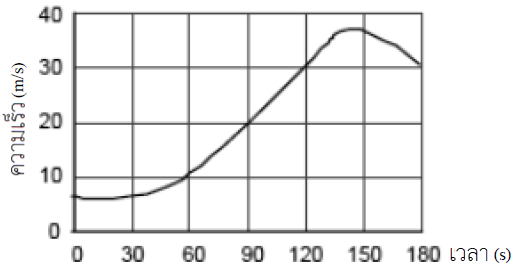
| 2. | กำหนดกราฟความเร็วเทียบกับเวลาของรถคันหนึ่ง อยากทราบว่า ความเร่งที่วินาทีที่ 90 เท่ากับข้อใด
 |
| A | 0.22 m/s2 |
| B | 0.33 m/s2 |
| C | 1.0 m/s2 |
| D | 9.8 m/s2 |
| E | 30 m/s2 |
ตอบ (B)
จากโจทย์เป็นกราฟ v-t ความเร่งที่ t ใดๆ จึงหาจากความชันของกราฟที่ t นั้นๆ
ประมาณช่วง t = 60 – 120 s เป็นเส้นตรง เลือกพิกัด (60,10) และ (120,30) จะได้
จากโจทย์เป็นกราฟ v-t ความเร่งที่ t ใดๆ จึงหาจากความชันของกราฟที่ t นั้นๆ
ประมาณช่วง t = 60 – 120 s เป็นเส้นตรง เลือกพิกัด (60,10) และ (120,30) จะได้
\(\begin{align*} {{\rm{a}}_{t\, = \,90}} &= \frac{{\Delta {\rm{v}}}}{{\Delta {\rm{t}}}}\\ &= \frac{{30 - 10}}{{120 - 60}}\\ &= \frac{{20}}{{60}}\\ &= 0.33\,\,{\rm{m/}}{{\rm{s}}^{\rm{2}}} \end{align*}\)
| 3. | ให้ตำแหน่งของวัตถุกำหนดจากฟังก์ชันของเวลา x = 8t – 3t2 โดย x มีหน่วยเมตร และ t ในหน่วยวินาที แล้วความเร็วเฉลี่ยในช่วง t = 1 ถึง t = 2 s เท่ากับข้อใด |
| A | - 2 m/s |
| B | - 1 m/s |
| C | - 0.5 m/s |
| D | 0.5 m/s |
| E | 1 m/s |
ตอบ (B)
ข้อนี้ถามความเร็วเฉลี่ย จะได้
ความเร็วเฉลี่ย = \(\dfrac{{\Delta {\rm{x}}}}{{\Delta {\rm{t}}}} = \dfrac{{{{\rm{x}}_2} - {{\rm{x}}_1}}}{{{{\rm{t}}_2} - {{\rm{t}}_1}}}\)
( ส่วนความเร็ว ณ ขณะใดๆ \(= \rm v(t)=\dfrac{{{\rm{dx}}}}{{{\rm{dt}}}} = \mathop {{\rm{lim}}}\limits_{\Delta {\rm{t}} \to 0} = \dfrac{{\Delta {\rm{x}}}}{{\Delta {\rm{t}}}}\) )ข้อนี้ถามความเร็วเฉลี่ย จะได้
\(\begin{align*} \frac{{\Delta {\rm{x}}}}{{\Delta {\rm{t}}}} &= \frac{{{{\rm{x}}_{{\rm{t = 2}}}} - {{\rm{x}}_{{\rm{t = 1}}}}}}{{2 - 1}}\\ &= \frac{{(8(2) - 3{{(2)}^2}) - (8(1) - 3{{(1)}^2})}}{{2 - 1}}\\ &= - 1\,\,{\rm{m/s}} \end{align*}\)
| 4. | วัตถุถูกปล่อยจากหยุดนิ่ง และเคลื่อนที่ได้ระยะทาง h ในวินาทีแรก จงหาระยะที่วัตถุเคลื่อนที่ได้ในวินาทีที่สอง |
| A | h |
| B | 2h |
| C | 3h |
| D | 4h |
| E | h2 |
ตอบ (C)
ถ้าปล่อยวัตถุจากหยุดนิ่ง แล้วเกิดการเคลื่อนที่แสดงว่ามีความเร่ง a เกิดขึ้น
จาก v(t) = at จะได้
ถ้าปล่อยวัตถุจากหยุดนิ่ง แล้วเกิดการเคลื่อนที่แสดงว่ามีความเร่ง a เกิดขึ้น
จาก v(t) = at จะได้
\({\rm{x(t)}} = \int {{\rm{v dt}} = \dfrac{1}{2}} {\rm{a}}{{\rm{t}}^{\rm{2}}}\)
สมมุติให้ x(0) = 0 จากโจทย์จะได้
\(\begin{array}{l} {\rm{x(t = 1)}} = \dfrac{1}{2}{\rm{a(1}}{{\rm{)}}^{\rm{2}}} = {\rm{h}}\\ {\rm{x(t = 2)}} = \dfrac{1}{2}{\rm{a(2}}{{\rm{)}}^{\rm{2}}} = 4{\rm{h}} \end{array}\)
ดังนั้น ในวินาทีที่ 2 วัตถุเคลื่อนที่ไปได้ \(\rm x(t = 2) – x(t = 1) = 4h – h =3h\)| 5. | มีลังใส่ของเล่นถูกวางนิ่งไว้บนรถเลื่อนหิมะคันหนึ่ง ขณะเดียวกันมีแรงดึงรถเลื่อนขึ้นเนินเขาด้วยอัตราเร็วที่เพิ่มขึ้นเรื่อยๆ โดยลังไม่ได้ถูกยึดกับรถเลื่อนไว้ แล้วข้อใดคือแรงที่จะต้องรองรับอัตราเร็วที่เพิ่มขึ้นของลังของเล่นขณะเคลื่อนที่ขึ้นเนินเขา |
| A | แรงเสียดทานสถิตของรถเลื่อนที่กระทำกับลังของเล่น |
| B | แรงตั้งฉากของพื้นหิมะที่กระทำกับรถเลื่อน |
| C | แรงตั้งฉากของรถเลื่อนที่กระทำกับลังของเล่น |
| D | แรงโน้มถ่วงที่กระทำต่อรถเลื่อน |
| E | ไม่มีแรงใดรองรับ |
ตอบ (A)
จากโจทย์ให้ลังใส่ของมีความเร่ง แสดงว่าต้องมีแรงที่กระทำกับลังเกิดขึ้น
เมื่อเขียนแผนภาพจะได้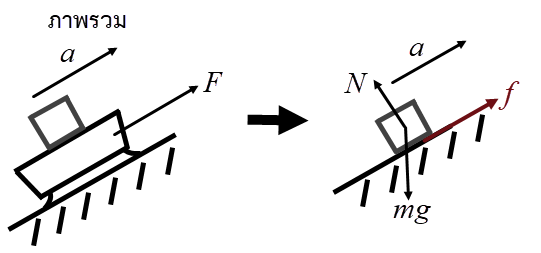 
สังเกตว่า มีแรงเสียดทานระหว่างลังกับเลื่อนหิมะ f เพียงแรงเดียวที่มีทิศเดียวกับ a (และทำให้ a เป็นบวก)
ดังนั้น มีแรงเสียดทานที่รองรับอัตราเร็วที่เพิ่มขึ้นของลังของเล่นขณะเคลื่อนที่ขึ้นเนินเขา
จากโจทย์ให้ลังใส่ของมีความเร่ง แสดงว่าต้องมีแรงที่กระทำกับลังเกิดขึ้น
เมื่อเขียนแผนภาพจะได้
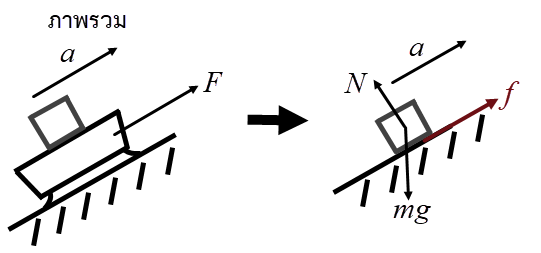
ดังนั้น มีแรงเสียดทานที่รองรับอัตราเร็วที่เพิ่มขึ้นของลังของเล่นขณะเคลื่อนที่ขึ้นเนินเขา
| 6. | ในเวลา t = 0 รถลาก เริ่มเคลื่อนที่จากหยุดนิ่งในแนวเส้นตรง ด้วยความเร็วตามฟังก์ชัน v = 5t2 , โดย v มีหน่วย m / s และ t มีหน่วย s ข้อใดแสดงการเคลื่อนที่ของรถจาก t = 0 ถึง t ได้ถูกต้องที่สุด |
| A | 5t3 |
| B | 5t3/3 |
| C | 10t |
| D | 15t2 |
| E | 5t/2 |
ตอบ (B)
จาก
จากเงื่อนไขเริ่มต้นให้ x(t = 0) = 0 จะได้
จาก
\(\begin{align*} {\rm{x}} &= \int {{\rm{v dt}}} \\ {\rm{x(t)}} &= \int\limits_{{\rm{t = 0}}}^{\rm{t}} {{\rm{5}}{{\rm{t}}^{\rm{2}}}{\rm{dt}}} \\ &= \dfrac{{\rm{5}}}{{\rm{3}}}{{\rm{t}}^{\rm{3}}}{\rm{ + c}} \end{align*}\)
( c เป็นค่าคงที่ )จากเงื่อนไขเริ่มต้นให้ x(t = 0) = 0 จะได้
\(\begin{array}{l} {\rm{0 = }}\dfrac{{\rm{5}}}{{\rm{3}}}{{\rm{t}}^{\rm{3}}}{\rm{ + c }}\\ {\rm{c = 0}} \end{array}\)
ดังนั้น \(\rm x(t) = \dfrac{{\rm{5}}}{{\rm{3}}}{{\rm{t}}^{\rm{3}}}\)| 7. | พลังงานศักย์ทางเคมีที่ถูกเก็บไว้ในแบตเตอรี่จะถูกแปลงเป็นพลังงานจลน์ที่ช่วยเพิ่มอัตราเร็วของรถของเล่นจาก 0 เป็น 2 ไมล์ต่อชั่วโมง แล้วเพิ่มจาก 2 เป็น 4 ไมล์ต่อชั่วโมง ถ้าไม่คำนึงถึงพลังงานที่กลายเป็นพลังงานความร้อนเนื่องจากแรงเสียดทาน และแรงต้านอากาศ แล้วข้อใดเปรียบเทียบพลังงานที่ต้องใช้ในการขับเคลื่อนจาก 2 เป็น 4 ไมล์ต่อชั่วโมงกับพลังงานที่ต้องใช้จาก 0 เป็น 2 ไมล์ต่อชั่วโมงได้ถูกต้องที่สุด |
| A | ใช้พลังงานเป็นครึ่งหนึ่ง |
| B | ใช้พลังงานเท่ากัน |
| C | ใช้พลังงานเป็นสองเท่า |
| D | ใช้พลังงานเป็นสามเท่า |
| E | ใช้พลังงานเป็นสี่เท่า |
ตอบ (D)
จากสูตรพลังงานจลน์
จะได้ Ek ที่ใช้เปลี่ยน v จาก 0 เป็น 2 ไมล์ต่อชั่วโมง เท่ากับ
จากสูตรพลังงานจลน์
\({{\rm{E}}_{\rm{k}}} = \dfrac{1}{2}{\rm{m}}{{\rm{v}}^2}\)
เมื่อ m = มวลวัตถุ , v = ความเร็ววัตถุจะได้ Ek ที่ใช้เปลี่ยน v จาก 0 เป็น 2 ไมล์ต่อชั่วโมง เท่ากับ
\({{\rm{E}}_{{\rm{k(0}} \to 2)}} = \dfrac{1}{2}{\rm{m(2}}{{\rm{)}}^2} - \dfrac{1}{2}{\rm{m(0}}{{\rm{)}}^2} = 2{\rm{m}}\)
และ Ek ที่ใช้เปลี่ยน v จาก 2 เป็น 4 ไมล์ต่อชั่วโมง เท่ากับ
\({{\rm{E}}_{{\rm{k(2}} \to 4)}} = \dfrac{1}{2}{\rm{m(4}}{{\rm{)}}^2} - \dfrac{1}{2}{\rm{m(2}}{{\rm{)}}^2} = 6{\rm{m}}\)
ดังนั้น \(\dfrac{{{{\rm{E}}_{{\rm{k(2}} \to 4)}}}}{{{{\rm{E}}_{{\rm{k(0}} \to 2)}}}} = \dfrac{{6{\rm{m}}}}{{2{\rm{m}}}} = 3\)| 8. | ถ้าดาวฤกษ์สองดวงอยู่ห่างกันมาก แล้วพลังงานศักย์โน้มถ่วงของทั้งสองเท่ากับศูนย์ ถ้าดาวทั้งสองดวงห่างกัน d พลังงานศักย์โน้มถ่วงของระบบจะเท่ากับ U แล้วดาวที่ห่างกัน 2d พลังงานศักย์โน้มถ่วงของระบบจะเท่ากับข้อใด |
| A | U/4 |
| B | U/2 |
| C | U |
| D | 2U |
| E | 4U |
ตอบ (B)
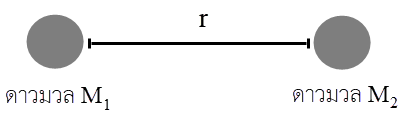จาก
จะได้ว่า
ดังนั้น
\({\rm{U}} = \dfrac{{ - {\rm{G}}{{\rm{M}}_{\rm{1}}}{{\rm{M}}_{\rm{2}}}}}{{\rm{r}}}\)
ดังนั้น \({\rm{U}} \propto \dfrac{1}{{\rm{r}}}\)จะได้ว่า
\(\dfrac{{{{\rm{U}}_{\rm{1}}}}}{{{{\rm{U}}_{\rm{2}}}}}{\rm{ = }}\dfrac{{{{\rm{r}}_{\rm{2}}}}}{{{{\rm{r}}_{\rm{1}}}}}\)
ให้ U1 = U, r1 = d และ r2 = 2dดังนั้น
\(\begin{array}{l} \dfrac{{\rm{U}}}{{{{\rm{U}}_{\rm{2}}}}}{\rm{ = }}\dfrac{{{\rm{2d}}}}{{\rm{d}}}\\ {{\rm{U}}_{\rm{2}}} = \dfrac{{\rm{U}}}{2} \end{array}\)
| 9. | ให้พื้นเอียงถูกวางอยู่บนพื้นลื่น และมีกล่องที่เดิมอยู่นิ่งค่อยๆ เลื่อนลงมาจากพื้นเอียงที่มีความขรุขระ แล้วการเคลื่อนที่ของจุดศูนย์กลางมวลของระบบกล่องและพื้นเอียงจะเป็นไปตามข้อใด |
| A | จะไม่มีการเคลื่อนที่เกิดขึ้น |
| B | มีการเคลื่อนที่ตามแนวนอนด้วยอัตราเร็วคงที่ |
| C | มีการเคลื่อนที่ตามแนวนอนด้วยอัตราเร็วที่เพิ่มขึ้นเรื่อยๆ |
| D | มีการเคลื่อนที่ตามแนวตั้งด้วยอัตราเร็วที่เพิ่มขึ้นเรื่อยๆ |
| E | มีการเคลื่อนที่ทั้งในแนวตั้ง และแนวนอน |
ตอบ (D)
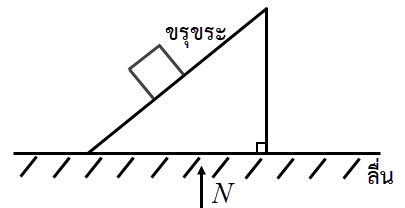หลักการ คือ จุดศูนย์กลางมวลจะเคลื่อนที่ได้เมื่อมีแรงภายนอกมากระทำ
พิจารณาแกน X : พื้นลื่นจึงไม่มีแรงเสียดทาน
ดังนั้น จุดศูนย์กลางมวลในแนวแกน X ไม่เคลื่อนที่
พิจารณาแกน Y : มีแรง N จากพื้นในทิศขึ้น
จาก
(เพิ่มเติม แรงเสียดทานระหว่างพื้นเอียงกับกล่องเป็นแรงภายใน จึงไม่ส่งผลต่อจุดศูนย์กลางมวลของทั้งระบบ)
พิจารณาแกน X : พื้นลื่นจึงไม่มีแรงเสียดทาน
ดังนั้น จุดศูนย์กลางมวลในแนวแกน X ไม่เคลื่อนที่
พิจารณาแกน Y : มีแรง N จากพื้นในทิศขึ้น
จาก
\(\begin{align*} \sum \rm F_y &= \rm ma_y\\ \rm a_y &> 0 \end{align*} \)
ดังนั้น จุดศูนย์กลางมวลจะเคลื่อนที่ในแนวแกน Y ด้วยความเร่ง(เพิ่มเติม แรงเสียดทานระหว่างพื้นเอียงกับกล่องเป็นแรงภายใน จึงไม่ส่งผลต่อจุดศูนย์กลางมวลของทั้งระบบ)
| 10. | ล้อมวล 1 kg สองวง มีแกนล้อคงที่ จากที่เดิมอยู่นิ่งมีแรงมากระทำ ดังรูป สมมุติว่า แกนล้อและซี่ล้อมีมวลเบามาก และความเฉื่อยในการหมุนเท่ากับ I = mR2 ถ้าต้องการให้ความเร่งเชิงมุมของทั้งสองล้อมีค่าเท่ากัน แล้วแรง F2 ที่กระทำบนแกนล้อควรเท่ากับข้อใด
 |
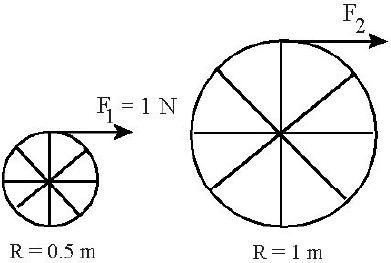| A | 0.25 N |
| B | 0.5 N |
| C | 1 N |
| D | 2 N |
| E | 4 N |
ตอบ (D)
จาก
พิจารณาล้อ 1 (R = 0.5 m)
ดังนั้น
จาก
\(\sum {\tau = {\rm{I}}\alpha } \)
พิจารณาล้อ 1 (R = 0.5 m)
\(\begin{align*} \rm F_1R &= \rm m_1^2\alpha \\ \rm{F}_1&= \rm mR_1\alpha \end{align*}\)
พิจารณาล้อ 2 (R = 1 m)
\({{\rm{F}}_{\rm{2}}}{\rm{ = m}}{{\rm{R}}_2}\alpha \)
ดังนั้น
\(\begin{array}{c} \dfrac{{{{\rm{F}}_{\rm{2}}}}}{{{{\rm{F}}_{\rm{1}}}}}{\rm{ = }}\dfrac{{{{\rm{R}}_{\rm{2}}}}}{{{{\rm{R}}_{\rm{1}}}}}\\ \dfrac{{{{\rm{F}}_{\rm{2}}}}}{1}{\rm{ = }}\dfrac{1}{{0.5}}\\ {{\rm{F}}_{\rm{2}}} = 2{\rm{N}} \end{array}\)
