หัวข้อฟิสิกส์ : มวล แรงและกฎการเคลื่อนที่
| 1. | ให้แผ่นกลม, ห่วง และทรงกลม มีมวล และรัศมีเท่ากัน และจะหมุนอย่างอิสระรอบแกนที่ผ่านจุดศูนย์กลางของวัตถุ โดยสมมุติว่าห่วงเชื่อมกับแกนหมุนด้วยซี่ล้อรถ ถ้าวัตถุที่เดิมอยู่นิ่ง ถูกกระทำที่วงด้านนอกด้วยแรงเดียวกัน ในเวลาเดียวกัน แล้วข้อใดจัดอันดับพลังงานจลน์ของวัตถุจากน้อยไปมาก หลังเวลาผ่านไป t ได้ถูกต้อง
 |
| A | แผ่นกลม, ห่วง, ทรงกลม |
| B | ทรงกลม, แผ่นกลม, ห่วง |
| C | ห่วง, ทรงกลม, แผ่นกลม |
| D | แผ่นกลม, ทรงกลม, ห่วง |
| E | ห่วง, แผ่นกลม, ทรงกลม |
ตอบ (E)
จากโจทย์ให้ทุกวัตถุถูกหมุนด้วย F เท่ากัน รัศมีเท่ากัน ดังนั้น ทอร์กต้องเท่ากัน
เนื่องจาก วัตถุที่มีโมเมนต์ความเฉื่อย (I) มาก จะหมุนช้า ทำให้พลังงานจลน์มีค่าน้อย
ดังนั้น การเรียงลำดับพลังงานจลน์จากน้อยไปมาก ต้องเรียงลำดับ I จากมากไปน้อย ดังนี้
จากโจทย์ให้ทุกวัตถุถูกหมุนด้วย F เท่ากัน รัศมีเท่ากัน ดังนั้น ทอร์กต้องเท่ากัน
เนื่องจาก วัตถุที่มีโมเมนต์ความเฉื่อย (I) มาก จะหมุนช้า ทำให้พลังงานจลน์มีค่าน้อย
ดังนั้น การเรียงลำดับพลังงานจลน์จากน้อยไปมาก ต้องเรียงลำดับ I จากมากไปน้อย ดังนี้
ห่วง (\({\rm{M}}{{\rm{R}}^{\rm{2}}}\)) , แผ่นกลม (\(\dfrac{1}{2}{\rm{M}}{{\rm{R}}^{\rm{2}}}\)) , ทรงกลม (\(\dfrac{2}{5}{\rm{M}}{{\rm{R}}^{\rm{2}}}\))
| 2. | หินหนัก 2 kg แขวนที่ปลายไม้เมตรสม่ำเสมอยาว 1 เมตร ด้วยเชือกเบา ถ้าไม้เมตรเกิดสมดุลเมื่อหินที่แขวนอยู่ อยู่ห่างจากจุดหมุนไป 0.20 m แล้วไม้เมตรมีมวลเท่าใด  |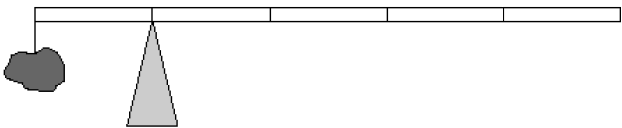
| A | 0.20 kg |
| B | 1.00 kg |
| C | 1.33 kg |
| D | 2.00 kg |
| E | 3.00 kg |
ตอบ (C)
ให้หินมีมวล m และไม้เมตรมีมวล M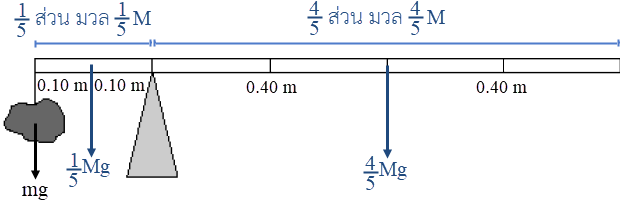
จากไม้เมตรเกิดสมดุลแสดงว่า
ให้หินมีมวล m และไม้เมตรมีมวล M
โมเมนต์ตาม \(=\) โมเมนต์ทวน
\(\begin{align*} \dfrac{4}{5}{\rm{Mg}}(0.40) &= \rm mg(0.20) + \dfrac{1}{5}{\rm{Mg}}(0.10)\\ \left( {\dfrac{4}{5}(0.40) - \dfrac{1}{5}(0.10)} \right)\rm M &= (0.20)(2)\\ \rm M &= \dfrac{4}{3} \end{align*}\)
ดังนั้น ไม้เมตรมีมวล \(\dfrac{4}{3} = 1.33 \rm ~~kg\)| 3. | ถ้าวัตถุหนึ่งเคลื่อนที่ไปตามแกน x พุ่งชนแบบยืดหยุ่นกับวัตถุแบบเดียวกันที่เดิมอยู่นิ่ง แล้วกราฟในข้อใดแสดงโมเมนตัม P เทียบกับเวลา t ของแต่ละวัตถุได้ถูกต้อง |
| A |  |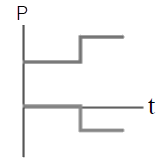
| B |  |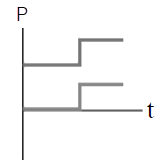
| C |  |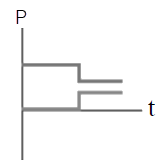
| D |  |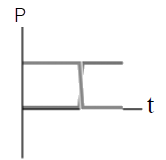
| E |  |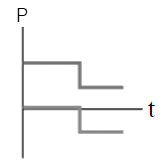
ตอบ (D)
โจทย์ให้เป็นการชนแบบยืดหยุ่นแสดงว่า
1) อนุรักษ์โมเมนตัม \(\sum \rm P\) ก่อนชน = \(\sum \rm P\)หลังชน
2) อนุรักษ์พลังงาน \(\rm E\)ก่อน = \(\rm E\)หลัง
พิจารณาจากเงื่อนไข 1)
จากกราฟจะเห็นว่า กราฟ (B), (E) มีการเปลี่ยนแปลงหลังชนไปในทำนองเดียวกัน (เพิ่มขึ้นเหมือนกัน หรือลดลงเหมือนกัน) ซึ่งขัดกับการอนุรักษ์โมเมนตัม
ดังนั้น กราฟ (B), (E) ไม่ใช่คำตอบ
และเมื่อวาดรูปจากกราฟ (A) จะได้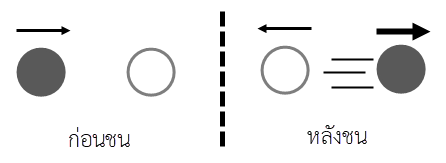
สังเกตว่า วัตถุที่อยู่นิ่งไม่ควรเด้งกลับหลังถูกชน
ดังนั้น กราฟ (A) ไม่ใช่คำตอบ
พิจารณาจากเงื่อนไข 2)
จากกราฟ (C)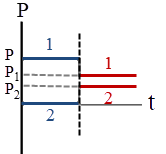
จากกราฟ (D)
ดังนั้น กราฟ (D) ถูกต้อง
โจทย์ให้เป็นการชนแบบยืดหยุ่นแสดงว่า
1) อนุรักษ์โมเมนตัม \(\sum \rm P\) ก่อนชน = \(\sum \rm P\)หลังชน
2) อนุรักษ์พลังงาน \(\rm E\)ก่อน = \(\rm E\)หลัง
พิจารณาจากเงื่อนไข 1)
จากกราฟจะเห็นว่า กราฟ (B), (E) มีการเปลี่ยนแปลงหลังชนไปในทำนองเดียวกัน (เพิ่มขึ้นเหมือนกัน หรือลดลงเหมือนกัน) ซึ่งขัดกับการอนุรักษ์โมเมนตัม
ดังนั้น กราฟ (B), (E) ไม่ใช่คำตอบ
และเมื่อวาดรูปจากกราฟ (A) จะได้
ดังนั้น กราฟ (A) ไม่ใช่คำตอบ
พิจารณาจากเงื่อนไข 2)
จากกราฟ (C)
\(\rm E\)ก่อน \(=\dfrac{1}{2}{\rm{m}}{{\rm{v}}^2} + 0 = \dfrac{1}{2}\dfrac{{{{\rm{m}}^2}{{\rm{v}}^2}}}{{\rm{m}}} = \dfrac{1}{2}\dfrac{{{{\rm{P}}^2}}}{{\rm{m}}}\)
\(\rm E\)หลัง \(=\dfrac{1}{2}{\rm{mv}}_1^2 + \dfrac{1}{2}{\rm{mv}}_2^2 = \dfrac{1}{2}\dfrac{{{\rm{P}}_1^{^2}}}{{\rm{m}}} + \dfrac{1}{2}\dfrac{{{\rm{P}}_2^{^2}}}{{\rm{m}}} = \dfrac{1}{{2{\rm{m}}}}\left( {{\rm{P}}_1^{^2} + {\rm{P}}_2^{^2}} \right)\)
จากกราฟสังเกตว่า \(\rm P_1 + P_2 \approx P\) แสดงว่า
\(\rm E\)ก่อน \(\approx \dfrac{1}{{2{\rm{m}}}}{\left( {{{\rm{P}}_1} + {{\rm{P}}_2}} \right)^2} = \dfrac{1}{{2{\rm{m}}}}({\rm{P}}_1^2 + {\rm{P}}_2^2 + 2{{\rm{P}}_1}{{\rm{P}}_2}) > \) \(\rm E\)หลัง
ซึ่งขัดกับการอนุรักษ์พลังงาน ดังนั้น กราฟ (C) ไม่ใช่คำตอบจากกราฟ (D)
\(\rm E\)ก่อน \(= \dfrac{1}{2}{\rm{m}}{{\rm{v}}^2} + 0 = \dfrac{1}{2}\dfrac{{{{\rm{P}}^2}}}{{\rm{m}}}\)
\(\rm E\)หลัง \(= 0 + \dfrac{1}{2}{\rm{m}}{{\rm{v}}^2} = \dfrac{1}{2}\dfrac{{{{\rm{P}}^2}}}{{\rm{m}}}\)
ซึ่ง \(\rm E\)ก่อน = \(\rm E\)หลังดังนั้น กราฟ (D) ถูกต้อง
| 4. | ให้อัตราเร็วของรถยนต์ที่มีระบบขับเคลื่อนล้อหลังมีขนาดเพิ่มขึ้น แล้วทิศทางของแรงเสียดทานบนยางรถยนต์จะเป็นไปตามข้อใด |
| A | ที่ล้อหน้ามีทิศถอยหลัง ที่ล้อหลังมีทิศไปข้างหน้า |
| B | ที่ล้อหน้ามีทิศไปข้างหน้า ที่ล้อหลังมีทิศถอยหลัง |
| C | ทุกล้อมีทิศไปข้างหน้า |
| D | ทุกล้อมีทิศถอยหลัง |
| E | แรงเสียดทานเป็นศูนย์ |
ตอบ (A)
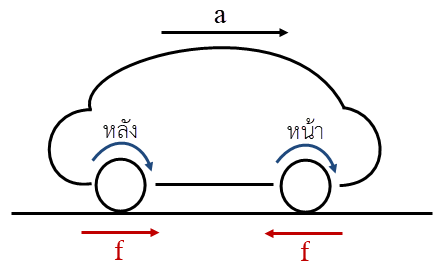ล้อหลัง : จะตะกุยพื้นเพื่อดันรถไปข้างหน้า ทำให้ล้อที่สัมผัสพื้นเคลื่อนที่ไปด้านหลัง \((\leftarrow)\) เทียบกับพื้น
ดังนั้น f ที่ต้านการเคลื่อนที่ของล้อหลังจะมีทิศไปข้างหน้า \((\rightarrow)\)
ล้อหน้า : เพลาของล้อหน้าจะเคลื่อนที่ไปข้างหน้า \((\rightarrow)\) ทำให้ล้อส่วนที่สัมผัสพื้นเคลื่อนที่ตามเพลา คือ ไปข้างหน้า \((\rightarrow)\) เทียบกับพื้น
ดังนั้น f ที่ต้านการเคลื่อนที่ของล้อหน้าจะมีทิศไปข้างหลัง \((\leftarrow)\)
ดังนั้น f ที่ต้านการเคลื่อนที่ของล้อหลังจะมีทิศไปข้างหน้า \((\rightarrow)\)
ล้อหน้า : เพลาของล้อหน้าจะเคลื่อนที่ไปข้างหน้า \((\rightarrow)\) ทำให้ล้อส่วนที่สัมผัสพื้นเคลื่อนที่ตามเพลา คือ ไปข้างหน้า \((\rightarrow)\) เทียบกับพื้น
ดังนั้น f ที่ต้านการเคลื่อนที่ของล้อหน้าจะมีทิศไปข้างหลัง \((\leftarrow)\)
| 5. | ให้แผ่นกลมสม่ำเสมอ (I = \(\dfrac{1}{2}\)MR2) มีมวล 8.0 kg สามารถหมุนรอบแกนโดยไม่มีแรงเสียดทาน และมีเชือกคล้องผ่านแผ่นกลมนั้น และแขวนมวล 6.0 kg เอาไว้ ดังรูป ถ้าเชือกไม่มีการไถล แล้วแรงตึงเชือกขณะมวลหย่อนลงมาเท่ากับข้อใด
 |
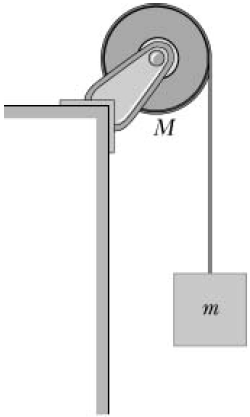| A | 20.0 N |
| B | 24.0 N |
| C | 34.3 N |
| D | 60.0 N |
| E | 80.0 N |
ตอบ (B)
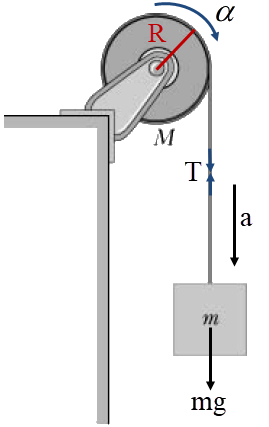โจทย์ให้ \(\rm M = 8.0 kg ,~ m = 6.0 kg\) ให้เชือกมีแรงตึง \(\rm T\)
พิจารณามวล \(\rm M\)
จาก \(\sum {\tau = {\rm{I}}\alpha }\)
จาก \(\sum {{\rm{F = ma}}}\)
พิจารณามวล \(\rm M\)
จาก \(\sum {\tau = {\rm{I}}\alpha }\)
\(\begin{align*} \rm TR &= \dfrac{{\rm{1}}}{{\rm{2}}}{\rm{M}}{{\rm{R}}^{\rm{2}}}\alpha \\ \alpha &= \dfrac{{{\rm{2T}}}}{{{\rm{MR}}}} \end{align*}\)
จากเงื่อนไขเชือกไม่ไถลทำให้
\(\rm a = \alpha \rm R = \left( {\dfrac{{{\rm{2T}}}}{{{\rm{MR}}}}} \right){\rm{R}} = \dfrac{{{\rm{2T}}}}{{\rm{M}}}\)
พิจารณามวล \(\rm m\)จาก \(\sum {{\rm{F = ma}}}\)
\({\rm{mg}} - {\rm{T = ma}}\)
แทน \({\rm{a = }}\dfrac{{{\rm{2T}}}}{{\rm{M}}}\) จะได้
\(\begin{align*} \rm mg - T &= m \dfrac{{{\rm{2T}}}}{{\rm{M}}}\\ \rm T &=\dfrac{{{\rm{mg}}}}{{1 + \dfrac{{{\rm{2m}}}}{{\rm{M}}}}}\\ &= \dfrac{{{\rm{6}}{\rm{.0(10)}}}}{{1 + \dfrac{{{\rm{2(6}}{\rm{.0)}}}}{{8.0}}}}\\ &= 24\,\,{\rm{N}} \end{align*}\)
ดังนั้น \(\rm T = 24 ~~N\)| 6. | ให้ลูกเบสบอลตกใส่ด้านบนของลูกบาส ขณะที่ลูกบาสกระแทกพื้นแล้วกระเด้งกลับด้วยอัตราเร็ว 4.0 m/s และพุ่งชนกับลูกเบสบอลที่ตกลงมาด้วยอัตราเร็ว 4.0 m/s หลังการชนลูกเบสบอลพุ่งกลับขึ้นไป ดังรูป และลูกบาสกลับมาอยู่นิ่งทันทีหลังการชน ถ้าลูกเบสบอลมวล 0.2 kg และลูกบาสมวล 0.5 kg และไม่สนแรงต้านอากาศ ไม่สนการดลเนื่องจากแรงโน้มถ่วง เพราะช่วงเวลาในการชนนั้นสั้นมาก แล้วอัตราเร็วของลูกเบสบอลหลังการชนกับลูกบาสที่พุ่งขึ้นมาเท่ากับข้อใด
 |
| A | 4.0 m/s |
| B | 6.0 m/s |
| C | 8.0 m/s |
| D | 12.0 m/s |
| E | 16.0 m/s |
ตอบ (B)
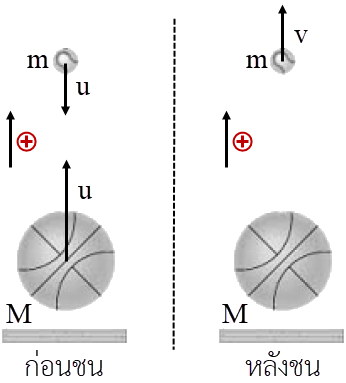โจทย์ให้ M = 0.5 kg, m = 0.2 kg, u = 4.0 m/s
ใช้หลักการอนุรักษ์โมเมนตัม (ในแนวดิ่ง)
ใช้หลักการอนุรักษ์โมเมนตัม (ในแนวดิ่ง)
ก่อนชน = หลังชน
\(\begin{align*} {\rm{Mu}} - {\rm{mu}} &= \rm M(0) + mv\\ {\rm{Mu}} - {\rm{mu}} &= \rm mv\\ v &= \left( {\frac{{{\rm{M}} - {\rm{m}}}}{{\rm{m}}}} \right){\rm{u}}\\ &= \left( {\frac{{0.5 - 0.2}}{{0.2}}} \right)4.0\\ &= 6.0\,\,{\rm{m/s}} \end{align*}\)
\(\begin{align*} {\rm{Mu}} - {\rm{mu}} &= \rm M(0) + mv\\ {\rm{Mu}} - {\rm{mu}} &= \rm mv\\ v &= \left( {\frac{{{\rm{M}} - {\rm{m}}}}{{\rm{m}}}} \right){\rm{u}}\\ &= \left( {\frac{{0.5 - 0.2}}{{0.2}}} \right)4.0\\ &= 6.0\,\,{\rm{m/s}} \end{align*}\)
| 7. | ให้วัตถุเล็กๆ ถูกขว้างไปออกจากตึกสูง 50.0 m ตามแนวนนอนด้วยอัตราเร็วต้น 10.0 m/s ตามแนววิถีที่วัตถุเคลื่อนที่ไปจะมีองค์ประกอบที่เป็นความเร่งที่สัมผัสกับแนววิถีการเคลื่อนที่ และความเร่งที่ตั้งฉากกับแนววิถี แล้วความเร่งของวัตถุในแนวสัมผัสกับแนวตั้งฉากจะมีค่าเท่ากัน หลังวัตถุถูกโยนออกไปกี่วินาที ไม่ต้องคำนึงถึงแรงต้านอากาศ |
| A | 2.00 s |
| B | 1.50 s |
| C | 1.00 s |
| D | 0.50 s |
| E | ที่ความสูงนั้นยังไม่สามารถทำให้เกิดเหตุการณ์นั้นได้ |
ตอบ (A)
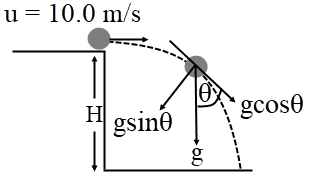จากรูป ความเร่งในแนวตั้งฉาก \(= \rm g\sin\theta\) และ ความเร่งในแนวสัมผัส \(=\rm g\cos\theta\)
โดยความเร่งในแนวตั้งฉาก \(=\) ความเร่งในแนวสัมผัส เมื่อ \(\rm g\sin\theta = g\cos\theta\)
ดังนั้น \(\tan\theta = 1\)
แสดงว่า \(\dfrac{{\rm{u}}}{{\rm{v}}} = \tan {\rm{\theta }} = 1\) ด้วย เมื่อ \(v\) เป็นความเร็วในแนวดิ่งของวัตถุ
จาก \(\rm v = gt\)
จาก
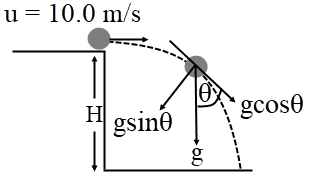
โดยความเร่งในแนวตั้งฉาก \(=\) ความเร่งในแนวสัมผัส เมื่อ \(\rm g\sin\theta = g\cos\theta\)
ดังนั้น \(\tan\theta = 1\)
แสดงว่า \(\dfrac{{\rm{u}}}{{\rm{v}}} = \tan {\rm{\theta }} = 1\) ด้วย เมื่อ \(v\) เป็นความเร็วในแนวดิ่งของวัตถุ
จาก \(\rm v = gt\)
\({\rm{t = }}\dfrac{{\rm{v}}}{{\rm{g}}}{\rm{ = }}\dfrac{{\rm{u}}}{{\rm{g}}} \approx \dfrac{{10.0}}{{10.0}} = 1.00\,\,{\rm{s}}\)
ตรวจสอบระยะทางที่ตก (s) จาก
\({\rm{s = }}\dfrac{{\rm{1}}}{{\rm{2}}}{\rm{g}}{{\rm{t}}^{\rm{2}}}{\rm{ = }}\dfrac{{\rm{1}}}{{\rm{2}}}{\rm{ \times 10 \times }}{{\rm{1}}^{\rm{2}}}{\rm{ = 5m < 50}}{\rm{.0m}}\)
ดังนั้น ความสูงเพียงพอที่จะทำให้เกิดเหตุการณ์นั้นได้| 8. | ก้อนน้ำแข็งเล็กๆ ที่เดิมอยู่นิ่ง ไหลลงมาตามแผ่นน้ำแข็งโค้งที่ไม่มีแรงเสียดทาน ดังรูป แล้วที่จุด A จะเป็นจุดเชื่อมแผ่นน้ำแข็งกับพื้นเอียงที่ยกขึ้นมา 30° จากแนวระดับ และมีสัมประสิทธิ์เสียดทาน μk ความยาวทางลาดยาว \(\dfrac{3}{2}\rm h\) ถ้าก้อนน้ำแข็งนิ่งสนิทที่ปลายด้านล่างของพื้นเอียง แล้ว μk เท่ากับข้อใด
 |
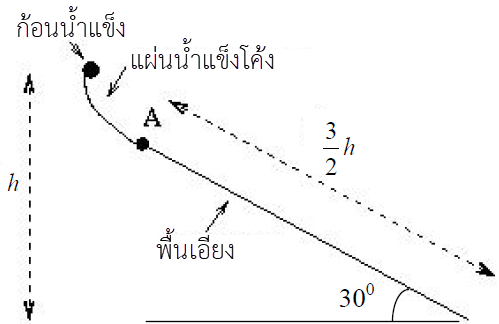| A | 0.866 |
| B | 0.770 |
| C | 0.667 |
| D | 0.385 |
| E | 0.333 |
ตอบ (B)
จากงานและพลังงาน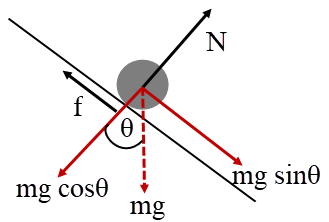
โดย \({\rm{f}} = {{\rm{\mu }}_{\rm{k}}}{\rm{N}} = {{\rm{\mu }}_{\rm{k}}}{\rm{mg}}\cos \theta \) จะได้ว่า
จากงานและพลังงาน
พลังงานศักย์โน้มถ่วง \(+\) งานที่แรงเสียดทานทำ (ติดลบ) \(= 0\) (น้ำแข็งหยุดนิ่งที่ปลายราง)
\(\rm mgh + \left( – f\left( {\dfrac{3}{2}{\rm{h}}} \right) \right)= 0\)
วาดรูปจากโจทย์
\(\rm mgh + \left( – f\left( {\dfrac{3}{2}{\rm{h}}} \right) \right)= 0\)
\(\begin{align*} \rm mgh &=\dfrac{{\rm{3}}}{{\rm{2}}}{\rm{fh}}\\ \rm mg &= \dfrac{{\rm{3}}}{{\rm{2}}}{\rm{(}}{{\rm{\mu }}_{\rm{k}}}{\rm{mg ~cos}}\theta {\rm{)}}\\ {{\rm{\mu }}_{\rm{k}}} &= \dfrac{{\rm{2}}}{{\rm{3}}}\dfrac{1}{{{\rm{cos30}}^\circ }}\\ &= \dfrac{4}{{3\sqrt 3 }}\\ &\approx 0.770 \end{align*}\)
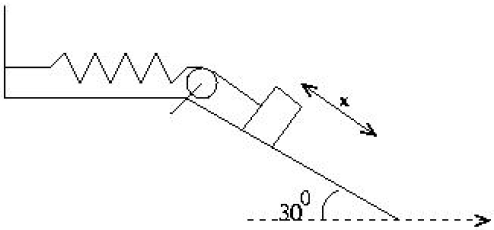
| 9. | ให้สปริงที่ไม่ได้เป็นไปตาม กฎของฮุค มีแรง F = – kx2 โดย k เป็นค่านิจสปริง x เป็นระยะสปริงที่ยังไม่ถูกยืดจากระบบที่แสดง ดังรูป ถ้านำวัตถุมวล m ติดกับสปริงที่เดิมอยู่นิ่ง แล้วระยะยืดของสปริงจนระบบหยุดนิ่งชั่วขณะเท่ากับข้อใด สมมุติว่า ทุกพื้นผิวและรอกไม่มีแรงเสียดทาน
 |
| A | \(\rm \left(\dfrac{3mg}{2k}\right)^{1/2}\) |
| B | \(\rm \left(\dfrac{mg}{k}\right)^{1/2}\) |
| C | \(\rm \left(\dfrac{2mg}{k}\right)^{1/2}\) |
| D | \(\rm \left(\dfrac{\sqrt3mg}{2k}\right)^{1/2}\) |
| E | \(\rm \left(\dfrac{3\sqrt3mg}{2k}\right)^{1/2}\) |
ตอบ (A)
จากโจทย์บอกระบบหยุดนิ่งชั่วขณะ แสดงว่าตอนนั้นระบบต้องไม่มีพลังงานจลน์
สมมุติให้วัตถุเคลื่อนที่ไปได้ระยะทาง x
ตอนสุดท้าย
เพิ่มเติม ข้อนี้ใช้สมดุลแรงไม่ได้ เพราะ ตรงจุดนี้วัตถุยังมีความเร็วอยู่ (Ek ≠ 0)
จากโจทย์บอกระบบหยุดนิ่งชั่วขณะ แสดงว่าตอนนั้นระบบต้องไม่มีพลังงานจลน์
สมมุติให้วัตถุเคลื่อนที่ไปได้ระยะทาง x
ตอนสุดท้าย
Eสปริง \(\displaystyle = - \int {{\rm{Fdx}} = - \left( { - \int {{\rm{k}}{{\rm{x}}^{\rm{2}}}{\rm{dx}}} } \right){\rm{ = }}\dfrac{{\rm{1}}}{{\rm{3}}}{\rm{k}}{{\rm{x}}^{\rm{3}}}} \)
ตอนแรก
Eศักย์ \(= {\rm{mg ~x}}\sin 30^\circ = \dfrac{1}{2}{\rm{mg ~x}}\)
จากกฎอนุรักษ์พลังงาน
\(\begin{align*} \dfrac{1}{3}{\rm{k}}{{\rm{x}}^3} &= \dfrac{1}{2}{\rm{mgx}}\\ \rm x &= \sqrt {\dfrac{3}{2}\dfrac{{{\rm{mg}}}}{{\rm{k}}}} \end{align*}\)
ดังนั้น ระยะยืดเท่ากับ \({\left( {\dfrac{{3{\rm{mg}}}}{{2{\rm{k}}}}} \right)^{\frac{1}{2}}}\) เพิ่มเติม ข้อนี้ใช้สมดุลแรงไม่ได้ เพราะ ตรงจุดนี้วัตถุยังมีความเร็วอยู่ (Ek ≠ 0)
Ek = Eศักย์ – Eสปริง = \(\dfrac{1}{2}{\rm{mg x}} - \dfrac{{\rm{1}}}{{\rm{3}}}{\rm{k}}{{\rm{x}}^{\rm{3}}} = \sqrt {\dfrac{1}{8}\dfrac{{{{\rm{m}}^{\rm{3}}}{{\rm{g}}^{\rm{3}}}}}{{\rm{k}}}} - \sqrt {\dfrac{1}{{24}}\dfrac{{{{\rm{m}}^{\rm{3}}}{{\rm{g}}^{\rm{3}}}}}{{\rm{k}}}} \ne 0\)
เพราะ สมดุลแรงบอกแค่ว่า a = 0 ไม่ได้บอกว่า v = 0 หรือไม่| 10. | จุดมวลเล็กๆ เคลื่อนที่ไปตามแนวนอนระหว่างผนังสองด้านที่ไม่มีแรงเสียดทาน ด้วยพลังงานจลน์เริ่มต้น E ทุกครั้งที่ชนกับผนัง มวลจะสูญเสียพลังงานจลน์ไป \(\dfrac{1}{2}\) ไปเป็นพลังงานความร้อน แล้ววัตถุจะชนกับผนังได้กี่ครั้ง ก่อนที่ความเร็วของมวลจะลดลงจนเหลือ \(\dfrac{1}{8}\) เท่าของของเดิม |
| A | 3 |
| B | 4 |
| C | 6 |
| D | 8 |
| E | 16 |
ตอบ (C)
จาก
v2, E2 เป็นความเร็ว (ที่ลดลงไป 8 เท่า) และพลังงาน ณ ขณะนั้น
จะได้
ดังนั้น ต้องชน 6 ครั้ง
\(\begin{array}{l} {{\rm{E}}_{\rm{k}}} = \dfrac{1}{2}{\rm{m}}{{\rm{v}}^2}\\ {{\rm{E}}_{\rm{k}}} \propto {{\rm{v}}^2} \end{array}\)
ให้ v1, E1 เป็นความเร็วและพลังงานตอนแรกv2, E2 เป็นความเร็ว (ที่ลดลงไป 8 เท่า) และพลังงาน ณ ขณะนั้น
จะได้
\(\rm \displaystyle \frac{{{E_2}}}{{{E_1}}} = \frac{{v_2^2}}{{v_1^2}} = {\left( {\frac{1}{8}} \right)^2} = {\left( {\frac{1}{2}} \right)^6}\)
