ข้อสอบคัดเลือกของทีม USA 2008 (25 ข้อ)
| 1. | นกบินเป็นเส้นตรง โดยเริ่มต้นบินด้วยอัตราเร็ว 10 m/s แล้วเพิ่มอัตราเร็วอย่างสม่ำเสมอจนถึง 18 m/s ได้ระยะทางทั้งหมด 40 m ความเร่งของนกเท่ากับข้อใด |
| A | 0.1 m/s2 |
| B | 0.2 m/s2 |
| C | 2.0 m/s2 |
| D | 2.8 m/s2 |
| E | 5.6 m/s2 |
ตอบ (D)
ให้เวลาผ่านไป t จาก \({\rm{a = }}\dfrac{{{\rm{\Delta v}}}}{{{\rm{\Delta t}}}}\) จะได้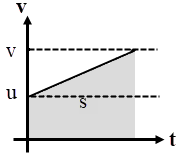 จาก s = พื้นที่สี่เหลี่ยมคางหมู
จาก s = พื้นที่สี่เหลี่ยมคางหมู
ให้เวลาผ่านไป t จาก \({\rm{a = }}\dfrac{{{\rm{\Delta v}}}}{{{\rm{\Delta t}}}}\) จะได้
\(\rm v – u = at\)
\(\rm t= \dfrac{{{\rm{v}} - {\rm{u}}}}{{\rm{a}}}\) --- (1)
จาก \({\rm{v = }}\dfrac{{{\rm{\Delta s}}}}{{{\rm{\Delta t}}}}\) ดังนั้น s เป็นพื้นที่ใต้กราฟ v – t

\(\rm s = \dfrac{1}{2}(v + u)t\)
จาก (1)
\(\begin{align*} {\rm{s}} &= \frac{1}{2}(v + u)(\frac{{v - u}}{{\rm{a}}})\\ a &= \frac{1}{2}\left( {\frac{{(v + u)(v - u)}}{{\rm{s}}}} \right) \end{align*}\)
แทนค่า
\(\begin{align*} a &= \frac{1}{2}\left( {\frac{{(18 + 10)(18 - 10)}}{{{\rm{40}}}}} \right)\\ &= \frac{1}{2}\left( {\frac{{8 \times 28}}{{{\rm{40}}}}} \right)\\ &= 2.8\,\,\,{\rm{m/}}{{\rm{s}}^{\rm{2}}} \end{align*}\)
| 2. | แมลงสาบไต่อยู่ภายในลูกบาศก์ที่มีความยาวด้าน 3 m ถ้าแมลงสาบเริ่มจากมุมซ้ายล่างที่ด้านหลังของลูกบาศก์ แล้วไต่มาถึงมุมบนขวาที่ด้านหน้าของลูกบาศก์ แล้วการกระจัดของแมลงสาบเท่ากับข้อใด |
| A | \(3\sqrt2 \rm ~m\) |
| B | \(3^3\sqrt2 \rm ~m\) |
| C | \(3\sqrt3 \rm ~m\) |
| D | \(\rm 3m\) |
| E | \(\rm 9m\) |
ตอบ (C)
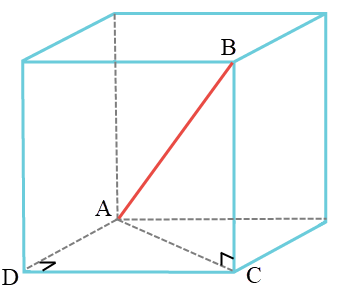 สามเหลี่ยม ADC
สามเหลี่ยม ADC

\(\begin{align*} {\rm{A}}{{\rm{C}}^{\rm{2}}} &= \rm A{{\rm{D}}^{\rm{2}}}{\rm{ + D}}{{\rm{C}}^{\rm{2}}}\\ {\rm{A}}{{\rm{C}}^{\rm{2}}} &= {{\rm{3}}^{\rm{2}}}{\rm{ + }}{{\rm{3}}^{\rm{2}}}{\rm{ = 18 }}{{\rm{m}}^{\rm{2}}} \end{align*}\)
สามเหลี่ยม ABC
\(\begin{align*} {\rm{A}}{{\rm{B}}^{\rm{2}}} &= A{{\rm{C}}^{\rm{2}}}{\rm{ + B}}{{\rm{C}}^{\rm{2}}}\\ {\rm{A}}{{\rm{B}}^{\rm{2}}} &= 18 +{{\rm{3}}^{\rm{2}}}{\rm{ = 27 }}{{\rm{m}}^{\rm{2}}} \end{align*}\)
ดังนั้น \(\rm AB = 3\sqrt3 \rm ~m\)| 3. | จากกราฟตำแหน่งเทียบกับเวลาของวัตถุที่เคลื่อนที่เป็นเส้นตรง ข้อใดคือความเร็ว ณ ขณะ t = 2 วินาที
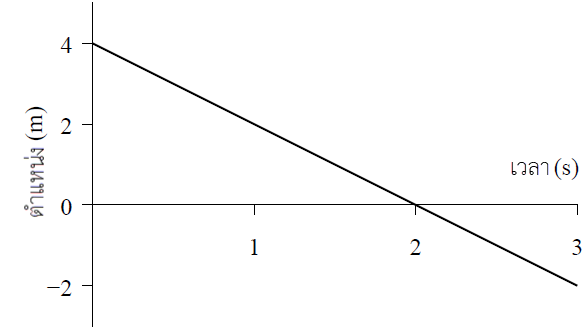 |
| A | \(-2 \rm ~m/s\) |
| B | \(-\dfrac{1}{2} \rm ~m/s\) |
| C | \(0\rm ~m/s\) |
| D | \(2\rm ~m/s\) |
| E | \(4\rm ~m/s\) |
ตอบ (A)
จาก \(\overrightarrow {\rm{v}} {\rm{ = }}\dfrac{{{\rm{\Delta }}\overrightarrow {\rm{s}} }}{{{\rm{\Delta t}}}}\)= slope
จาก \(\overrightarrow {\rm{v}} {\rm{ = }}\dfrac{{{\rm{\Delta }}\overrightarrow {\rm{s}} }}{{{\rm{\Delta t}}}}\)= slope
slope = \(\dfrac{{0 - 4}}{{2 - 0}} = - 2\)
ดังนั้น \(\rm v = – 2 m/s\)| 4. | กำหนดกราฟความเร็วเทียบกับเวลาของรถของเล่นที่เคลื่อนที่เป็นเส้นตรง
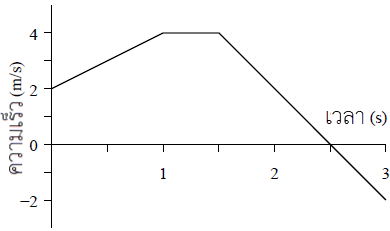 |
| A | 3 m |
| B | 5 m |
| C | 6.5 m |
| D | 7 m |
| E | 7.5 m |
ตอบ (D)
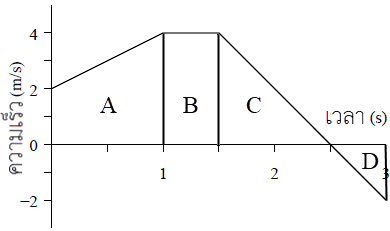

การกระจัด (S) = พื้นที่ใต้กราฟ v – t
Smax = พื้นที่ A + B + C
\(\begin{align*} &=\rm \dfrac{1}{2} (2 + 4)(1) + (0.5)(4) + \dfrac{1}{2} (1)(4) m\\ &= \rm3 + 2 + 2 m\\ &= \rm 7 m\end{align*}\)
เพิ่มเติม : บริเวณพื้นที่ D วัตถุหยุดนิ่งแล้ววิ่งกลับ ทำให้การกระจัดลดลง
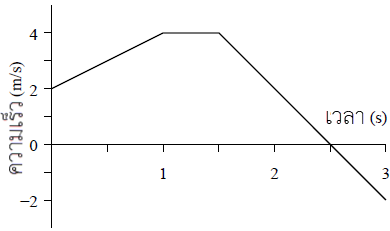
| 5. | กำหนดกราฟความเร็วเทียบกับเวลาของรถของเล่นที่เคลื่อนที่เป็นเส้นตรง
 |
| A | 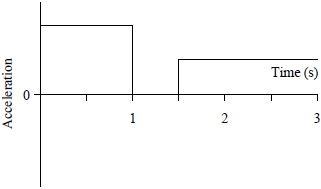 |
| B | 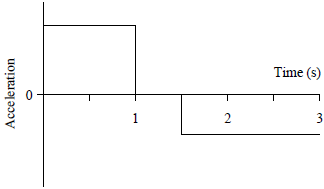 |
| C | 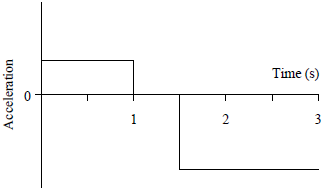 |
| D | 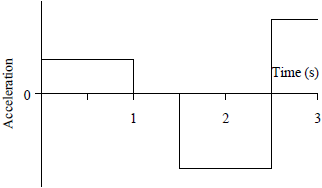 |
| E | 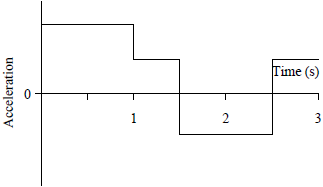 |
ตอบ (C)
จาก \(\overrightarrow {\rm{a}} {\rm{ = }}\dfrac{{{\rm{\Delta }}\overrightarrow {\rm{v}} }}{{{\rm{\Delta t}}}}=\rm slpoe\) กราฟ v – t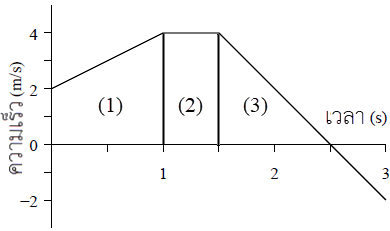
\(\begin{align*} {\rm{slop}}{{\rm{e}}_1} &= \frac{{4 - 2}}{{1 - 0}} = 2\,\,\,{\rm{m/}}{{\rm{s}}^2}\\ {\rm{slop}}{{\rm{e}}_2} &= 0\,\,\,{\rm{m/}}{{\rm{s}}^2}\\ {\rm{slop}}{{\rm{e}}_3} &= \frac{{0 - 4}}{{2.5 - 1.5}} = - 4\,\,\,{\rm{m/}}{{\rm{s}}^2} \end{align*}\)
วาดกราฟ a - t ได้ดังรูป
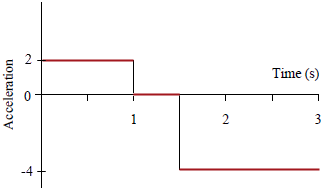
จาก \(\overrightarrow {\rm{a}} {\rm{ = }}\dfrac{{{\rm{\Delta }}\overrightarrow {\rm{v}} }}{{{\rm{\Delta t}}}}=\rm slpoe\) กราฟ v – t

\(\begin{align*} {\rm{slop}}{{\rm{e}}_1} &= \frac{{4 - 2}}{{1 - 0}} = 2\,\,\,{\rm{m/}}{{\rm{s}}^2}\\ {\rm{slop}}{{\rm{e}}_2} &= 0\,\,\,{\rm{m/}}{{\rm{s}}^2}\\ {\rm{slop}}{{\rm{e}}_3} &= \frac{{0 - 4}}{{2.5 - 1.5}} = - 4\,\,\,{\rm{m/}}{{\rm{s}}^2} \end{align*}\)
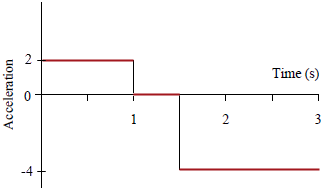
| 6. | ปืนใหญ่ยิงกระสุนแบบโพรเจกไทล์บนพื้นราบ โดยยิงทำมุมขนาดต่างๆ ด้วยอัตราเร็วเดียวกัน ถ้าระยะตกไกลสุดของกระสุนในแนวราบเท่ากับ L แล้วระยะตกของกระสุนที่ยิงทำมุม \(\dfrac{\pi}{6}\) กับแนวราบ เท่ากับข้อใด ไม่ต้องคิดแรงต้านอากาศ |
| A | \(\dfrac{\sqrt 3}{2}\rm L\) |
| B | \(\dfrac{1}{\sqrt 2}\rm L\) |
| C | \(\dfrac{1}{\sqrt 3}\rm L\) |
| D | \(\dfrac{1}{2}\rm L\) |
| E | \(\dfrac{1}{3}\rm L\) |
ตอบ (A)
 จะหา D
จะหา D
พิจารณา sy หา t ที่ใช้จากจุดเริ่มต้น \(\to\) จุดสุดท้าย
จาก
ดังนั้น \(\rm L = \dfrac{{{{\rm{v}}^{\rm{2}}}}}{{\rm{g}}}\)
จากโจทย์ แทน θ = \(\pi\)/6 จะได้

พิจารณา sy หา t ที่ใช้จากจุดเริ่มต้น \(\to\) จุดสุดท้าย
จาก
\(\begin{align*} {{\rm{s}}_{\rm{y}}} &= {{\rm{v}}_{\rm{y}}}{\rm{t}} - \frac{1}{2}{\rm{g}}{{\rm{t}}^{\rm{2}}}\\
0 &= {{\rm{v}}_{\rm{y}}}{\rm{t}} - \dfrac{1}{2}{\rm{g}}{{\rm{t}}^{\rm{2}}}\\ \rm t &= \dfrac{{{\rm{2}}{{\rm{v}}_{\rm{y}}}}}{{\rm{g}}} = \dfrac{{{\rm{2vsin\theta }}}}{{\rm{g}}} \end{align*}\)
จะได้
\(\begin{align*} \rm D &= {{\rm{v}}_{\rm{x}}}{\rm{t}}\\
&= \left( {{\rm{v cos\theta }}} \right)\left( {\frac{{{\rm{2v}}}}{{\rm{g}}}{\rm{sin\theta }}} \right)\\
&= \dfrac{{{\rm{2}}{{\rm{v}}^2}}}{{\rm{g}}}{\rm{sin\theta cos\theta }}\\
&= \dfrac{{{{\rm{v}}^2}}}{{\rm{g}}}{\rm{sin2\theta }} \end{align*}\)
จะได้ Dmax เมื่อ sin2θ = 1 (θ = \(\pi\)/4 นั่นเอง) ดังนั้น \(\rm L = \dfrac{{{{\rm{v}}^{\rm{2}}}}}{{\rm{g}}}\)
จากโจทย์ แทน θ = \(\pi\)/6 จะได้
\({\rm{D = }}\,\,\dfrac{{{{\rm{v}}^2}}}{{\rm{g}}}{\rm{sin}}\left( {{\rm{2}} \cdot \dfrac{\pi }{6}} \right)\,\, = \,\,{\rm{L~sin}}\left( {\dfrac{\pi }{3}} \right)\,\, = \,\,\dfrac{{\sqrt 3 }}{2}{\rm{L}}\)
| 7. | เลื่อนหิมะเคลื่อนที่ด้วยอัตราเร็ว 2.0 m/s บนพื้นหิมะ ให้คนและเลื่อนมีมวลรวมกัน 120 kg และเด็กอีกคน (mเด็ก = 40 kg) พุ่งเข้ามาในทิศตรงข้ามกับเลื่อนหิมะ แล้วกระโดดขึ้นเลื่อนจากทางด้านหน้า ถ้าเด็กคนนั้นมีอัตราเร็วก่อนขึ้นไปบนเลื่อน 5.0 m/s แล้วอัตราเร็วใหม่ของเลื่อนจะเท่ากับข้อใด ไม่ต้องคิดผลของแรงเสียดทาน |
| A | 0.25 m/s |
| B | 0.33 m/s |
| C | 2.75 m/s |
| D | 3.04 m/s |
| E | 3.67 m/s |
ตอบ (A)
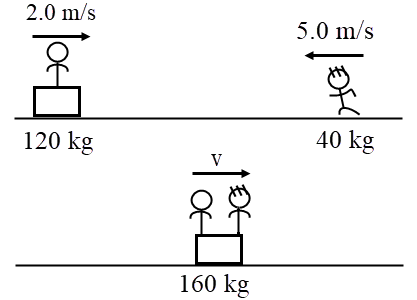 จากกฎอนุรักษ์โมเมนตัม
จากกฎอนุรักษ์โมเมนตัม
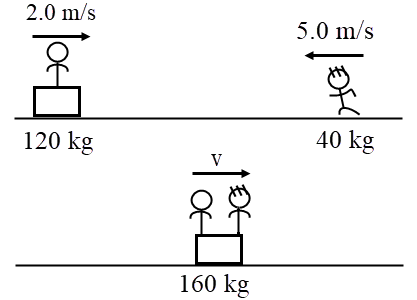
\(\begin{align*} (120)(2.0) + (40)( - 5.0) &= 160v\\ 240 - 200 &= 160v\\ v &= 0.25 \rm ~~m/s \end{align*} \)
| 8. | ชายคนหนึ่งเล่นเครื่องเล่นโดยหันหลังพิงกับกำแพงของถังทรงกระบอกที่มีเส้นผ่าศูนย์กลาง 8.0 m ถ้าถังหมุนรอบแกนที่ผ่านศูนย์กลางในอัตรา 45 รอบ/นาที แล้วนำพื้นใต้เท้าที่ชายคนนั้นยืนอยู่ออกไป จงหาค่าสัมประสิทธิ์แรงเสียดทานสถิตระหว่างกำแพงกับชายคนนั้นที่น้อยที่สุดที่ทำให้เขาไม่หล่นลงไป |
| A | 0.0012 |
| B | 0.056 |
| C | 0.11 |
| D | 0.53 |
| E | 8.9 |
ตอบ (C)
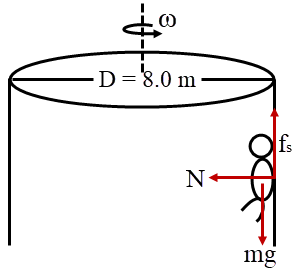 จาก 45 รอบ/นาที = \(\dfrac{{45 \times 2\pi }}{{60}}\) rad / s = \(\dfrac{3}{2}\pi \) s-1
จาก 45 รอบ/นาที = \(\dfrac{{45 \times 2\pi }}{{60}}\) rad / s = \(\dfrac{3}{2}\pi \) s-1
คนไม่หล่นลงไป
แต่ fs ≤ μsN จะได้

คนไม่หล่นลงไป
fs = mg --- (1)
การเคลื่อนที่แบบวงกลม
N = mω2R --- (2)
แต่ fs ≤ μsN จะได้
\(\begin{align*} {\rm{mg}} &\le {{\rm{\mu }}_{\rm{s}}}{\rm{m}}{{\rm{\omega }}^{\rm{2}}}{\rm{R}}\\ {{\rm{\mu }}_{\rm{s}}} &\ge \frac{{\rm{g}}}{{{{\rm{\omega }}^{\rm{2}}}{\rm{R}}}} \sim \frac{{10}}{{{{\left( {\frac{3}{2}\pi } \right)}^2}\left( {\frac{8}{2}} \right)}} = \frac{{10}}{{9{\pi ^2}}} = 0.11 \end{align*}\)
| 9. | บอลมวล m1 เคลื่อนที่ในทิศบวกตามแกน x ด้วยอัตราเร็วต้น v0 แล้วชนกับบอลมวล m2 ซึ่งเดิมอยู่นิ่ง หลังจากการชน บอลมวล m1 มีความเร็ว v1x \(\hat x\) + v1y\(\hat y\) และบอลมวล m2 มีความเร็ว v2x \(\hat x\) + v2y\(\hat y\) จงพิจารณาข้อความต่อไปนี้
I) 0 = m1v1x + m1v2x
II) m1v0 = m1v1y +m2v2y
III) 0 = m1v1y + m2v2y
IV) m1v0 = m1v1x + m1v1y
V) m1v0 = m1v1x + m2v2x
ข้อใดสอดคล้องกับระบบ |
| A | I และ II |
| B | III และ V |
| C | II และ V |
| D | III และ IV |
| E | I และ III |
ตอบ (B)
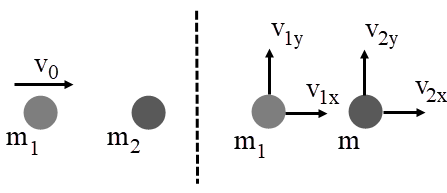 จากกฎอนุรักษ์โมเมนตัม
จากกฎอนุรักษ์โมเมนตัม
แนวแกน x
แนวแกน y
ดังนั้น III และ V สอดคล้องกับระบบ

แนวแกน x
m1v0 = m1v1x + m2v2x
ตรงกับข้อ (V)แนวแกน y
0 = m1v1x + m2v2y
ตรงกับข้อ (III)ดังนั้น III และ V สอดคล้องกับระบบ
| 10. | จากการทดลองลากกล่องไม้หนักๆ ที่วางอยู่บนพื้นด้วยเครื่องชั่งสปริง ได้บันทึกแรงที่ใช้ในแต่ละครั้งกับความเร่งของบล็อกไม้ ดังนี้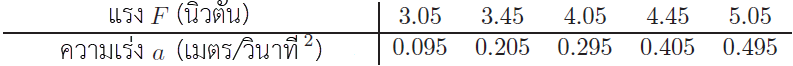 แล้วมวลของกล่องไม้ควรเท่ากับข้อใด |
| A | 3 kg |
| B | 5 kg |
| C | 10 kg |
| D | 20 kg |
| E | 30 kg |
ตอบ (B)
เขียนสมการนิวตัน
จากข้อมูล เมื่อนำมาวาดกราฟ จะได้ f = 2.52 N และ m = 4.98 \(\approx\) 5 kg
เขียนสมการนิวตัน
\(\begin{align*} {\rm{F}} - {\rm{f}} &= {\rm{ma}}\\ {\rm{F}} &= {\rm{ma}} + {\rm{f}} \end{align*}\)
จะได้ m เป็น slope และ f เป็น จุดตัดแกน yจากข้อมูล เมื่อนำมาวาดกราฟ จะได้ f = 2.52 N และ m = 4.98 \(\approx\) 5 kg
| 11. | จากการทดลองลากกล่องไม้หนักๆ ที่วางอยู่บนพื้นด้วยเครื่องชั่งสปริง ได้บันทึกแรงที่ใช้ในแต่ละครั้งกับความเร่งของบล็อกไม้ ดังนี้
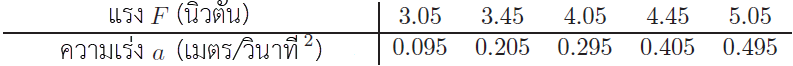 |
| A | 0.05 |
| B | 0.07 |
| C | 0.09 |
| D | 0.5 |
| E | 0.6 |
ตอบ (A)
เขียนสมการนิวตัน
จากข้อมูล เมื่อนำมาวาดกราฟ จะได้ f = 2.52 N และ m = 4.98
จาก f = μN
เขียนสมการนิวตัน
\(\begin{align*} {\rm{F}} - {\rm{f}} &= {\rm{ma}}\\ {\rm{F}} &= {\rm{ma}} + {\rm{f}} \end{align*}\)
จะได้ m เป็น slope และ f เป็น จุดตัดแกน yจากข้อมูล เมื่อนำมาวาดกราฟ จะได้ f = 2.52 N และ m = 4.98
จาก f = μN
\(\begin{align*} f &=\rm \mu N\\ \mu &=\rm \frac{f}{{mg}} = \frac{{2.52}}{{4.98 \times 10}} \approx 0.05 \end{align*}\)
| 12. | แผ่นกลมสม่ำเสมอหมุนด้วยความเร็วเชิงมุมคงที่รอบแกนที่ผ่านศูนย์กลาง และตั้งฉากกับระนาบแผ่นกลม และมีพลังงานจลน์เท่ากับ E ถ้าแผ่นกลมแบบเดียวกันหมุนด้วยความเร็วเชิงมุมเดียวกัน แต่หมุนรอบแกนที่ขอบของแผ่นกลม (แกนยังคงตั้งฉากกับระนาบแผ่นกลม) แล้วพลังงานจลน์จะมีค่าเท่ากับข้อใด |
| A | \(\dfrac{1}{2}\rm E\) |
| B | \(\dfrac{3}{2}\rm E\) |
| C | \(2\rm E\) |
| D | \(3\rm E\) |
| E | \(4\rm E\) |
ตอบ (D)
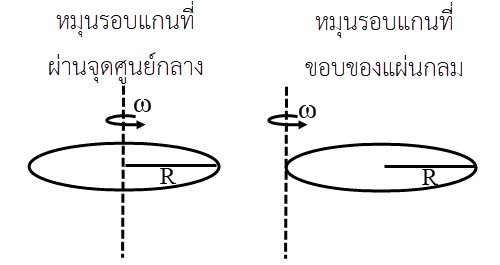 กรณี หมุนที่จุดศูนย์กลาง
กรณี หมุนที่จุดศูนย์กลาง
พลังงานจลน์การหมุน = \(\dfrac{1}{2}{\rm{m}}{{\rm{R}}^{\rm{2}}}\)
แผ่นกลม \({\rm{I}} = \dfrac{1}{2}{\rm{m}}{{\rm{R}}^{\rm{2}}}\)
จากทฤษฎีแกนขนาน
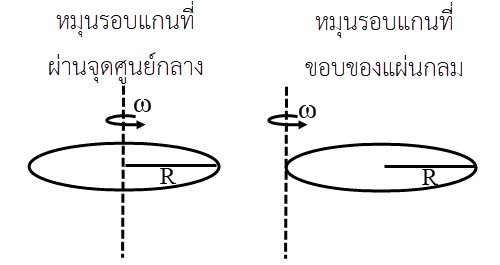
พลังงานจลน์การหมุน = \(\dfrac{1}{2}{\rm{m}}{{\rm{R}}^{\rm{2}}}\)
แผ่นกลม \({\rm{I}} = \dfrac{1}{2}{\rm{m}}{{\rm{R}}^{\rm{2}}}\)
\({\rm{E = }}\dfrac{{\rm{1}}}{{\rm{2}}}\left( {\dfrac{{\rm{1}}}{{\rm{2}}}{\rm{m}}{{\rm{R}}^{\rm{2}}}} \right){{\rm{\omega }}^{\rm{2}}}\)
กรณี หมุนที่ขอบของวงกลมจากทฤษฎีแกนขนาน
\(\rm I_{ขอบ} = I + mR^2 = \dfrac{1}{2}mR^2 + mR^2 = \dfrac{3}{2}mR^2\)
จะได้
\(\rm E_{ขอบ} = \dfrac{1}{2}(I_{ขอบ}) ω^2 = \dfrac{1}{2}(\dfrac{3}{2}mR^2) ω^2\)
ดังนั้น \(\rm E_{ขอบ} = 3E\)| 13. | ติดมวลก้อนหนึ่งกับผนังด้วยสปริงที่มีค่านิจสปริง k ขณะสปริงมีความยาวตามปกติ มวลจะได้รับความเร็วต้นค่าหนึ่ง ทำให้สปริงสั่นด้วยแอมพลิจูด A ถ้าเปลี่ยนสปริงให้มีค่านิจสปริง 2k และมวลได้รับความเร็วต้นเท่าเดิม แล้วแอมพลิจูดของการสั่นเท่ากับข้อใด |
| A | \(\dfrac{1}{2}\rm A\) |
| B | \(\dfrac{1}{\sqrt 2}\rm A\) |
| C | \(\sqrt{2}\rm A\) |
| D | \(2\rm A\) |
| E | \(2\rm A\) |
ตอบ (B)
 ถ้าสปริงยืดที่ระยะ x = A สปริงจะมีความเร็ว = 0 (ถ้ายังวิ่งต่อ ก็ไม่ใช่ระยะมากที่สุด)
ถ้าสปริงยืดที่ระยะ x = A สปริงจะมีความเร็ว = 0 (ถ้ายังวิ่งต่อ ก็ไม่ใช่ระยะมากที่สุด)
ให้ความเร็วต้น = v
จากกฎอนุรักษ์พลังงาน

ให้ความเร็วต้น = v
จากกฎอนุรักษ์พลังงาน
\(\begin{array}{l} \dfrac{1}{2}{\rm{m}}{{\rm{v}}^2} = \dfrac{1}{2}{\rm{k}}{{\rm{A}}^2}\\ \,\,\,\,\,\therefore {\rm{A}} \propto \dfrac{{\rm{v}}}{{\sqrt {\rm{k}} }} \end{array}\)
ถ้าเปลี่ยน k \(\to\) 2k โดย v คงที่ จะได้
\(\begin{align*} \frac{{{\rm{A'}}}}{{\rm{A}}} &= \sqrt {\frac{{\rm{k}}}{{{\rm{2k}}}}} \\ \rm A' &=\frac{{\rm{A}}}{{\sqrt {\rm{2}} }} \end{align*}\)
| 14. | เครื่องกักเก็บพลังงานประกอบด้วย มวลที่เหมือนกันสองชิ้นที่เชื่อมกันด้วยเชือก และจะหมุนรอบจุดศูนย์กลางมวล โดยพลังงานที่ถูกเพิ่มเข้ามาจะถูกเก็บไว้โดยการม้วนพันเชือกให้เชือกระหว่างมวลมีความยาวลดลง โดยไม่มีแรงภายนอกมากระทำ ถ้าเดิมเครื่องมีพลังงานจลน์ E และหมุนด้วยความเร็วเชิงมุม ω จากนั้นเพิ่มพลังงานจนเครื่องหมุนด้วยความเร็วเชิงมุม 2ω แล้วพลังงานจลน์ของเครื่องนี้จะมีค่าเท่ากับข้อใด |
| A | \(\sqrt 2\rm E\) |
| B | \(2\rm E\) |
| C | \(2\sqrt 2\rm E\) |
| D | \(4\rm E\) |
| E | \(8\rm E\) |
ตอบ (B)
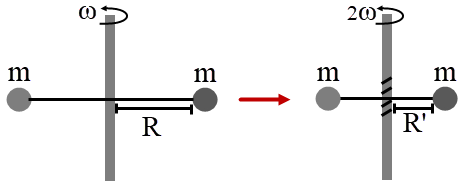 การเพิ่มพลังงานช่วยให้เชือกหด แรงทั้งหมดผ่านแกนเชือก
การเพิ่มพลังงานช่วยให้เชือกหด แรงทั้งหมดผ่านแกนเชือก
ดังนั้น อนุรักษ์โมเมนตัมเชิงมุมรอบจุดศูนย์กลาง

ดังนั้น อนุรักษ์โมเมนตัมเชิงมุมรอบจุดศูนย์กลาง
\(\rm L = mωR^2 =\) ค่าคงที่
ดังนั้น
\(\begin{align*} {\rm{m\omega }}{{\rm{R}}^2} &= {\rm{m(2w)}}{{{\rm{R'}}}^2}\\ \rm {{R'}^2} &= \frac{{{{\rm{R}}^2}}}{2} \end{align*}\)
จะได้
\(\begin{align*} \rm E' &=\frac{{\rm{1}}}{{\rm{2}}}{\rm{I'}}{{{\rm{\omega '}}}^{\rm{2}}}\\ &= \frac{{\rm{1}}}{{\rm{2}}}\left( {{\rm{m}}{{{\rm{R'}}}^{\rm{2}}}} \right){{{\rm{\omega '}}}^{\rm{2}}}\\ &= \frac{{\rm{1}}}{{\rm{2}}}\left( {{\rm{m}}\frac{{{{\rm{R}}^{\rm{2}}}}}{{\rm{2}}}} \right){{\rm{(2\omega )}}^{\rm{2}}}\\ &= \frac{{\rm{1}}}{{\rm{2}}} \cdot 4\left( {\frac{1}{2}{\rm{m}}{{\rm{R}}^2}{{\rm{\omega }}^{\rm{2}}}} \right)\\ &= 2{\rm{E}} \end{align*}\)
ดังนั้น \({\rm{E'}} = 2{\rm{E}}\)| 15. | โต๊ะกลมสม่ำเสมอมีเส้นผ่านศูนย์กลาง 4.0 m มวล 50.0 kg มีขาโต๊ะที่เบามากสูง 1.0 m และห่างกัน 3.0 m ถ้าช่างไม้คนหนึ่งไปนั่งที่ขอบโต๊ะ แล้วมวลมากสุดของช่างไม้ ที่ทำให้โต๊ะไม่กระดกเท่ากับข้อใด สมมุติว่าแรงที่ช่างไม้กระทำตั้งฉากกับโต๊ะ และกระทำที่ขอบโต๊ะเท่านั้น
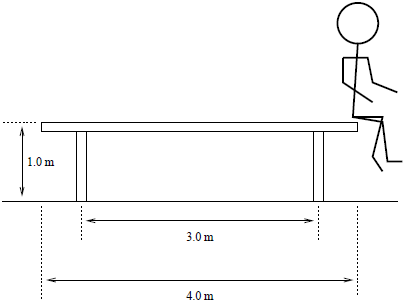 |
| A | 67 kg |
| B | 75 kg |
| C | 81 kg |
| D | 150 kg |
| E | 350 kg |
ตอบ (D)
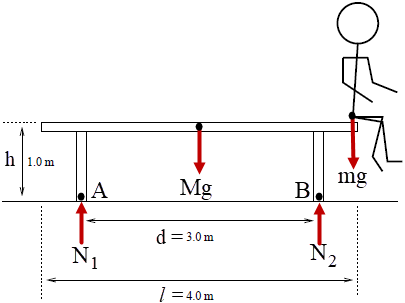 สมการนิวตัน
สมการนิวตัน

\(\rm mg + Mg = N_1 + N_2\)
สมดุลทอร์ก จุดหมุนที่ A
\({\rm{Mg}}\dfrac{{\rm{d}}}{{\rm{2}}}{\rm{ + mg}}\left( {{\rm{d }} + \dfrac{{l - {\rm{d}}}}{2}} \right) = {{\rm{N}}_{\rm{2}}}{\rm{d}}\)
เงื่อนไขพื้นไม่กระดก (กระดกพอดี ถ้าช่างมวลมากที่สุด)
\(\rm N_1 = 0\)
จะได้ว่า
\(\begin{align*} {\rm{Mg}}\frac{{\rm{d}}}{{\rm{2}}}{\rm{ + mg}}\left( {{\rm{d }} + \frac{{l - {\rm{d}}}}{2}} \right) &= {{\rm{N}}_{\rm{2}}}{\rm{d = (m + M)gd}}\\ {\rm{mg}}\left( {\frac{{l - {\rm{d}}}}{2}} \right) &= \frac{1}{2}{\rm{Mgd}} \end{align*}\)
ดังนั้น \(\rm {\rm{m = }}\left( {\dfrac{{\rm{d}}}{{l - {\rm{d}}}}} \right){\rm{M}} = \dfrac{{3.0}}{{4.0 - 1.0}}(50.0) = 150~kg\)| 16. | สปริงเบาที่มีค่านิจสปริง k ถูกจับตั้งขึ้นให้ปลายด้านหนึ่งติดอยู่กับพื้น ส่วนปลายด้านบนปล่อยอิสระ ถ้าปล่อยลูกบอลมวล m จากแนวตั้งให้ลงไปติดกับสปริง กล่าวคือ ลูกบอลพุ่งชนกับสปริงในแนวตั้ง แล้วเกิดการสั่นในแนวตั้ง ให้ y เป็นความสูงวัดจากปลายสปริงตอนที่ยังไม่ยืดไม่หด จงหาความเร่ง a ของมวลขณะที่สั่นและอยู่ที่ความสูง y เหนือปลายสปริงตอนที่ยังไม่ยืดไม่หด และให้ทิศลงเป็นลบ โดยไม่ต้องคิดแรงต้านอากาศ กำหนดให้ g คือ ความเร่งในการตกอย่างอิสระ และ v คือ อัตราเร็วที่ตำแหน่งนั้น |
| A | a = mv2/y + g |
| B | a = mv2/k – g |
| C | a = (k/m)y – g |
| D | a = – (k/m)y + g |
| E | a = – (k/m)y – g |
ตอบ (E)
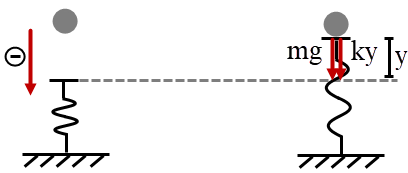 จากกฎของนิวตัน
จากกฎของนิวตัน

\(\begin{align*} - {\rm{mg}} - {\rm{ky}} &= {\rm{ma}}\\ {\rm{a}} &= - \frac{{\rm{k}}}{{\rm{m}}}{\rm{y}} - {\rm{g}} \end{align*}\)
| 17. | มวล m อยู่นิ่ง ณ จุดสมดุล ขณะถูกแขวนในแนวตั้งบนสปริงที่เดิมยาว L มีค่านิจสปริง k ดังรูป
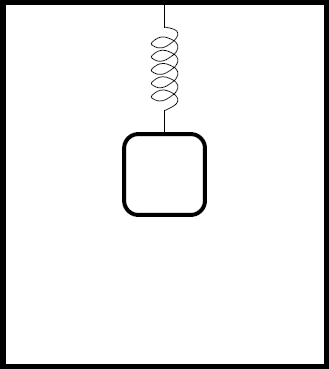 |
| A | (a/g)L |
| B | (g/a)L |
| C | m(g + a)/k |
| D | m(g – a)/k |
| E | ma/k |
ตอบ (E)
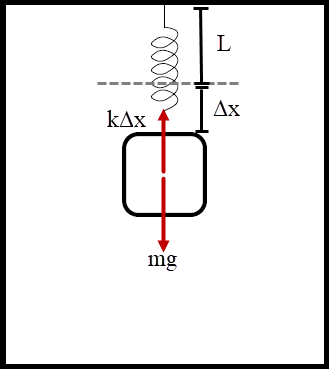
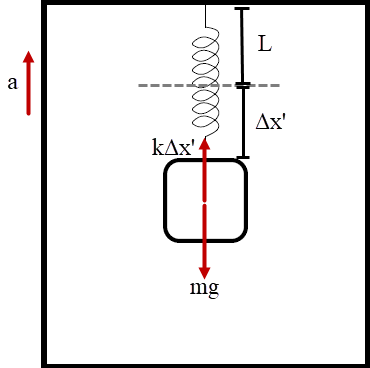 เมื่อแขวนมวล m สปริงจะยืดจนถึงจุดสมดุล
เมื่อแขวนมวล m สปริงจะยืดจนถึงจุดสมดุล
ให้จุดสมดุล สปริงยืด \(\Delta {\rm{x}}\) จะได้
จาก (1) และ (2)


ให้จุดสมดุล สปริงยืด \(\Delta {\rm{x}}\) จะได้
\({\rm{mg = k}}\Delta {\rm{x}}\) --- (1)
เมื่อลิฟต์มีความเร่ง a ทิศขึ้น สปริงจะยืดมากขึ้น จาก \(\Delta {\rm{x}}\) เป็น \(\Delta {\rm{x'}}\) จะได้\({\rm{ k}}\Delta {\rm{x'}}-{\rm{mg = ma}}\) --- (2)
จาก (1) และ (2)
\(\begin{align*} {\rm{k}}\Delta {\rm{x'}}-{\rm{k}}\Delta \rm x &= \rm ma\\ \left( {\Delta {\rm{x'}}-\Delta {\rm{x}}} \right) &= \dfrac{{{\rm{ma}}}}{{\rm{k}}} \end{align*}\)
| 18. | วงแหวนสม่ำเสมอ รัศมี R อยู่คงที่ที่จุดหนึ่ง และให้อนุภาคหนึ่งอยู่ในแนวแกนกลางวงแหวนในระยะที่ไกลมาก ( เทียบกับ R ) และสามารถเข้าไปสู่วงแหวนด้วยอิทธิพลจากแรงโน้มถ่วงของวงแหวนได้ โดยอนุภาคนั้นจะมีอัตราเร็วสูงสุด v ถ้าเราเปลี่ยนวงแหวน ให้มีความหนาแน่นเชิงเส้นเท่าเดิม แต่มีรัศมี 2R แล้วทำการทดลองซ้ำ แล้วอัตราเร็วสูงสุดใหม่ของอนุภาคจะเท่ากับข้อใด |
| A | \(\dfrac{1}{2}\rm v\) |
| B | \(\dfrac{1}{\sqrt2}\rm v\) |
| C | \(\rm v\) |
| D | \(\sqrt2\rm v\) |
| E | \(2\rm v\) |
ตอบ (C)
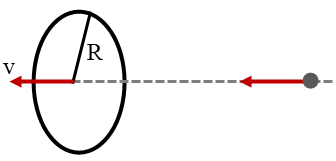 ให้วงแหวนมีความหนาแน่นเชิงเส้น = \(\lambda \)
ให้วงแหวนมีความหนาแน่นเชิงเส้น = \(\lambda \)
อนุภาค (ณ ใดๆ) มีพลังงาน = 0
อนุภาค (ณ ความเร็วสูงสุด) มีพลังงาน = Ekmax + Ep
เมื่อ Ekmax คือ พลังงานจลน์ของวัตถุ ณ ความเร็วสูงสุด
Ep คือ พลังงานศักย์โน้มถ่วงที่เกิดจากวงแหวน ขณะที่วัตถุมีความเร็วสูงสุด
จากกฎอนุรักษ์พลังงาน
Ep น้อยสุด เมื่อวัตถุอยู่ใกล้วงแหวนมากที่สุด นั่นคือ กำลังผ่านจุดศูนย์กลางของวงแหวน
ดังนั้น ถ้าเปลี่ยนจาก R เป็น 2R ความเร็วสูงสุดของวัตถุก็ยังคงเป็น v

อนุภาค (ณ ใดๆ) มีพลังงาน = 0
อนุภาค (ณ ความเร็วสูงสุด) มีพลังงาน = Ekmax + Ep
เมื่อ Ekmax คือ พลังงานจลน์ของวัตถุ ณ ความเร็วสูงสุด
Ep คือ พลังงานศักย์โน้มถ่วงที่เกิดจากวงแหวน ขณะที่วัตถุมีความเร็วสูงสุด
จากกฎอนุรักษ์พลังงาน
Ekmax + Ep = 0
Ep = – Ekmax = มีค่าน้อยสุด
Ep น้อยสุด เมื่อวัตถุอยู่ใกล้วงแหวนมากที่สุด นั่นคือ กำลังผ่านจุดศูนย์กลางของวงแหวน
\({{\rm{E}}_{{\rm{p min}}}} = - \dfrac{{{\rm{GMm}}}}{{\rm{R}}} = - \dfrac{{{\rm{Gm(2\pi R\lambda }})}}{{\rm{R}}} = - {\rm{2\pi \lambda mG}}\)
จะได้
\(- \dfrac{1}{2}{\rm{m}}{{\rm{v}}^2} = - 2{\rm{\pi \lambda mG}}\)
นั่นคือ v ไม่ขึ้นกับ Rดังนั้น ถ้าเปลี่ยนจาก R เป็น 2R ความเร็วสูงสุดของวัตถุก็ยังคงเป็น v
| 19. | รถคันหนึ่งมีเครื่องยนต์ที่ให้กำลังคงที่ เมื่อเร่งเครื่องจากที่เดิมอยู่นิ่ง ที่เวลา t = 0 และมีความเร่งเท่ากับ a0 ที่เวลา t = t0 แล้วความเร่งที่ t = 2t0 เท่ากับข้อใด ไม่ต้องคำนึงพลังงานที่สูญเสียไปกับแรงเสียดทาน |
| A | \(\dfrac{1}{2}\rm a_0\) |
| B | \(\dfrac{1}{\sqrt2}\rm a_0\) |
| C | \(\rm a_0\) |
| D | \(\sqrt2\rm a_0\) |
| E | \(2\rm a_0\) |
ตอบ (B)
ให้กำลังของรถยนต์ = P
จะได้
แทน a1 = a0 , t1 = t0 , t2 = 2t0 เพื่อหา a2
จะได้
ให้กำลังของรถยนต์ = P
จะได้
\({\rm{Pt = }}\dfrac{{\rm{1}}}{{\rm{2}}}{\rm{m}}{{\rm{v}}^{\rm{2}}}\)
เมื่อ t คือ เวลาที่รถยนต์แล่นจากหยุดนิ่ง
\(\begin{align*}
\rm v(t) &= \rm \sqrt {\frac{{2P}}{m}t} \\
\rm a(t) &= \rm \dfrac{{dv}}{{dt}} = \dfrac{1}{2}\sqrt {\frac{{2P}}{{mt}}} \\
\rm a &\propto \rm \dfrac{1}{{\sqrt t }}
\end{align*}\)
ดังนั้น \(\dfrac{{{{\rm{a}}_{\rm{1}}}}}{{{{\rm{a}}_{\rm{2}}}}}{\rm{ = }}\sqrt {\dfrac{{{{\rm{t}}_{\rm{2}}}}}{{{{\rm{t}}_{\rm{1}}}}}} \)แทน a1 = a0 , t1 = t0 , t2 = 2t0 เพื่อหา a2
จะได้
\(\begin{align*}
\frac{{{{\rm{a}}_{\rm{0}}}}}{{{{\rm{a}}_{\rm{2}}}}} &= \sqrt {\rm{2}} \\
{{\rm{a}}_{\rm{2}}} &= \frac{1}{{\sqrt {\rm{2}} }}{{\rm{a}}_{\rm{0}}}
\end{align*}\)
| 20. | ให้มอดุลัสของยังมีค่าเท่ากับ E ซึ่งค่านี้จะใช้วัดความแข็งของวัสดุ ถ้าวัสดุนั้นมีค่า E มากกว่า วัสดุนั้นก็จะมีความแข็งมากกว่า ลองพิจารณาคานเหล็กหน้าตัดสี่เหลี่ยมมุมฉาก ที่ปลายด้านหนึ่งถูกตรึงตามแนวนอนกับกำแพง และสามารถเอียงตามน้ำหนักของตัวคานได้ ถ้าคานยาว L, หนา h, กว้าง w, ความหนาแน่น ρ, และมอดุลัสของยังเท่ากับ E ความเร่งโน้มถ่วงเท่ากับ g แล้วระยะทางที่ปลายอีกข้างหนึ่งเคลื่อนที่ไปจะเท่ากับข้อใด (คำแนะนำ: อาจจะใช้การตัดตัวเลือกที่ไม่น่าจะเป็นได้ออกก่อน ซึ่งตัวเลือกทั้งหมดมีหน่วยถูกต้อง) |
| A | \(\rm h ~exp\left(\dfrac{ρgL}{E}\right)\) |
| B | \(\rm 2\dfrac{ρgL^2}{E}\) |
| C | \(\rm \sqrt{2Lh}\) |
| D | \(\rm \dfrac{3}{2}\dfrac{ρgL^4}{Eh^2}\) |
| E | \(\rm \sqrt{3}\dfrac{EL}{\rho gh}\) |
ตอบ (D)
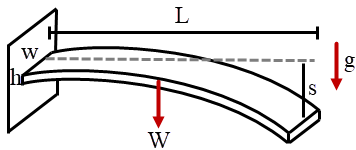 กำหนดให้ s เป็นระยะทางที่ปลายเหล็กเคลื่อนที่
กำหนดให้ s เป็นระยะทางที่ปลายเหล็กเคลื่อนที่
(1) ถ้า E มาก วัสดุจะแข็งแรง ทำให้ การงอ \(\downarrow ~\to\) s \(\downarrow\) (ตัดข้อ C,E)
(2) ถ้า L มาก จะทำให้ s \(\uparrow\) เพราะเหล็กยาว น้ำหนักเหล็กยิ่งมาก เหล็กจะเบนได้มากกว่า (ไม่มีการตัดข้อเพิ่ม)
(3) ถ้า h มาก จะทำให้ s \(\downarrow\) เพราะผนังมีแรง N ทำกับคาน ยิ่ง h มาก ทอร์กของแรง N ก็ยิ่งมากทำให้ช่วยพยุงแท่งเหล็กได้ดี s จึงน้อย (ตัดข้อ A,B)
ดังนั้น ข้อ (D) เป็นไปได้มากที่สุด

(1) ถ้า E มาก วัสดุจะแข็งแรง ทำให้ การงอ \(\downarrow ~\to\) s \(\downarrow\) (ตัดข้อ C,E)
(2) ถ้า L มาก จะทำให้ s \(\uparrow\) เพราะเหล็กยาว น้ำหนักเหล็กยิ่งมาก เหล็กจะเบนได้มากกว่า (ไม่มีการตัดข้อเพิ่ม)
(3) ถ้า h มาก จะทำให้ s \(\downarrow\) เพราะผนังมีแรง N ทำกับคาน ยิ่ง h มาก ทอร์กของแรง N ก็ยิ่งมากทำให้ช่วยพยุงแท่งเหล็กได้ดี s จึงน้อย (ตัดข้อ A,B)
ดังนั้น ข้อ (D) เป็นไปได้มากที่สุด
| 21. | พิจารณาอนุภาคที่เดิมอยู่นิ่ง แล้วแตกตัวออกเป็นสองอนุภาค หรือสามอนุภาค แล้วข้อใดต่อไปนี้เป็นจริงสำหรับการแตกตัวเป็นสองอนุภาค แต่เป็นเท็จสำหรับการแตกตัวเป็นสามอนุภาค (ไม่มีแรงภายนอกใดมากระทำ) |
| A | เวกเตอร์ความเร็วของอนุภาคที่แตกออกมาจะอยู่ในระนาบเดียวเท่านั้น |
| B | ถ้ากำหนดพลังงานจลน์สุทธิของระบบ และมวลของแต่ละอนุภาคที่แตกออกมาให้ ก็สามารถหาอัตราเร็วของแต่ละอนุภาคได้ |
| C | ถ้ากำหนดอัตราเร็วของทั้งหมด แต่ไม่บอกของหนึ่งอนุภาคที่แตกออกมาให้ ก็สามารถหาอัตราเร็วของอนุภาคที่เหลือได้ |
| D | โมเมนตัมรวมของอนุภาคที่แตกออกมาจะเท่ากับศูนย์ |
| E | ไม่มีข้อใดถูก |
ตอบ (B)
| ข้อ | แตกเป็น 2 อนุภาค | แตกเป็น 3 อนุภาค |
| (A) | เป็นจริง เพราะ 2 เวกเตอร์ จะอยู่ในระนาบเดียวกันเสมอ | เป็นจริง เพราะ ในกรณีที่มี 2 เวกเตอร์อยู่ในระนาบเดียวกัน แต่เวกเตอร์ที่ 3 ไม่อยู่ในระนาบดังกล่าว ก็จะเกิด component ของเวกเตอร์ในแนวตั้งฉากกับระนาบ ทำให้ผลรวมเวกเตอร์ไม่มีทางเป็น 0 ดังนั้น เวกเตอร์ความเร็ว 3 เวกเตอร์ ต้องอยู่ในระนาบเดียวกัน |
| (B) | เป็นจริง เพราะ จากกฎอนุรักษ์โมเมนตัม
m1v1 = m2v2
และพลังงานรวม
\({\rm{E = }}\dfrac{{\rm{1}}}{{\rm{2}}}{{\rm{m}}_{\rm{1}}}{\rm{v}}_{\rm{1}}^{\rm{2}} + \dfrac{{\rm{1}}}{{\rm{2}}}{{\rm{m}}_{\rm{2}}}{\rm{v}}_2^{\rm{2}}\)
สังเกตว่า 2 สมการ 2 ตัวแปร สามารถหาความเร็วของแต่ละอนุภาคได้ |
เป็นเท็จ เพราะ จากกฎอนุรักษ์โมเมนตัม
m1v1 + m2v2 + m3v3 = 0
และพลังงานรวม
\({\rm{E = }}\displaystyle\sum\limits_{i = 1}^3 {\frac{{\rm{1}}}{{\rm{2}}}{{\rm{m}}_{\rm{i}}}{\rm{v}}_i^{\rm{2}}}\)
สังเกตว่า 2 สมการ มากกว่า 2 ตัวแปร ไม่สามารถหาความเร็วของแต่ละอนุภาคได้ |
| (C) | เป็นเท็จ เพราะจากกฎอนุรักษ์โมเมนตัม
\(\begin{align*} {{\rm{m}}_{\rm{1}}}{{\rm{v}}_{\rm{1}}} &= {{\rm{m}}_{\rm{2}}}{{\rm{v}}_{\rm{2}}}\\ {{\rm{v}}_{\rm{2}}} &= \frac{{{{\rm{m}}_{\rm{2}}}}}{{{{\rm{m}}_{\rm{1}}}}}{{\rm{v}}_{\rm{1}}} \end{align*}\)
ถ้าไม่ทราบ m1, m2 ก็ไม่สามารถหา v2 |
เป็นเท็จ เพราะจากกฎอนุรักษ์โมเมนตัม
\({{\rm{m}}_{\rm{1}}}{\overrightarrow {\rm{v}} _{\rm{1}}}{\rm{ + }}{{\rm{m}}_{\rm{2}}}{\overrightarrow {\rm{v}} _{\rm{2}}}{\rm{ + }}{{\rm{m}}_{\rm{3}}}{\overrightarrow {\rm{v}} _{\rm{3}}}{\rm{ = 0}}\)
ทราบเพียงขนาดของ \({\overrightarrow {\rm{v}} _{\rm{1}}}\) และ \({\overrightarrow {\rm{v}} _{\rm{2}}}\)ไม่ทราบ m1, m2, m3 และทิศทางของ \({\overrightarrow {\rm{v}} _{\rm{1}}},{\overrightarrow {\rm{v}} _{\rm{2}}},{\overrightarrow {\rm{v}} _{\rm{3}}}\) จึงไม่สามารถหาขนาดของ \({\overrightarrow {\rm{v}} _{\rm{3}}}\) ได้ |
| (D) | เป็นจริง เพราะไม่มีแรงภายนอกมากระทำ จึงใช้กฎอนุรักษ์โมเมนตัมได้ ดังนั้น โมเมนตัมรวมของอนุภาคที่แตกออกมาจะเท่ากับศูนย์ |
เป็นจริง เพราะไม่มีแรงภายนอกมากระทำ จึงใช้กฎอนุรักษ์โมเมนตัมได้ ดังนั้น โมเมนตัมรวมของอนุภาคที่แตกออกมาจะเท่ากับศูนย์ |
| 22. | กระสุนมวล m1 ชนกับลูกตุ้มมวล m2 ที่ห้อยลงมาจากเชือกยาว L ด้วยความเร็วตามแนวนอน v0 ถ้าการชนนี้ไม่ยืดหยุ่นสมบูรณ์และกระสุนฝังเข้าด้านในลูกตุ้ม แล้วความเร็วต่ำสุดของ v0 ที่ทำให้ลูกตุ้ม (พร้อมกระสุนที่อยู่ภายใน) หมุนวนเป็นวงกลมตามแนวตั้งเท่ากับข้อใด |
| A | \(\rm 2\sqrt{Lg}\) |
| B | \(\rm \sqrt{5Lg}\) |
| C | \(\rm (m_1+m_2)2\sqrt{Lg}/m_1\) |
| D | \(\rm (m_1-m_2)\sqrt{Lg}/m_2\) |
| E | \(\rm (m_1+m_2)\sqrt{5Lg}/m_1\) |
ตอบ (E)
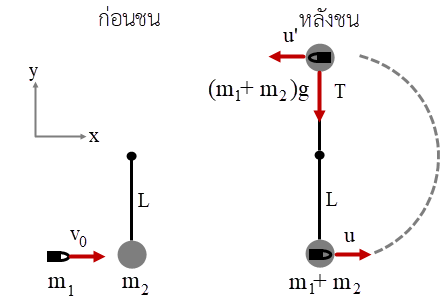 จากกฎอนุรักษ์โมเมนตัมแนวแกน x
จากกฎอนุรักษ์โมเมนตัมแนวแกน x
จะได้
จากกฎอนุรักษ์พลังงาน
จากสมการเคลื่อนที่วงกลม
ถ้าต้องการ v0 ต่ำสุดที่ทำให้มวล m1, m2 วนครบรอบ ต้องให้ T = 0 ณ จุดสูงสุด (เชือกกำลังหย่อนพอดี)
จะได้

จะได้
\(\rm m_1v_0 = (m_1 + m_2)u\)
\({\rm{u = }}\dfrac{{{{\rm{m}}_{\rm{1}}}}}{{{{\rm{m}}_{\rm{1}}}{\rm{ + }}{{\rm{m}}_{\rm{2}}}}}{{\rm{v}}_{\rm{0}}}\) --- (1)
พิจารณา ก้อน m1 กับ m2 ณ จุดสูงสุดของวงกลม ให้ก้อนดังกล่าวมีความเร็ว \(\rm{u'}\)จากกฎอนุรักษ์พลังงาน
\(\begin{align*} \frac{1}{2}{\rm{(}}{{\rm{m}}_{\rm{1}}}{\rm{ + }}{{\rm{m}}_{\rm{2}}}{\rm{)}}{{{\rm{u'}}}^{\rm{2}}}{\rm{ + (}}{{\rm{m}}_{\rm{1}}}{\rm{ + }}{{\rm{m}}_{\rm{2}}}\rm)g(2L) &= \frac{1}{2}{\rm{(}}{{\rm{m}}_{\rm{1}}}{\rm{ + }}{{\rm{m}}_{\rm{2}}}{\rm{)}}{{\rm{u}}^{\rm{2}}}\\ \frac{1}{2}{{{\rm{u'}}}^{\rm{2}}}\rm + g2L &= \frac{1}{2}{{\rm{u}}^{\rm{2}}} \end{align*}\)
\({{\rm{u'}}^{\rm{2}}} = {{\rm{u}}^{\rm{2}}} - 4{\rm{gL }}\) --- (2)
จากสมการเคลื่อนที่วงกลม
\({\rm{ (}}{{\rm{m}}_{\rm{1}}}{\rm{ + }}{{\rm{m}}_{\rm{2}}}{\rm{)g + T = }}\dfrac{{{\rm{(}}{{\rm{m}}_{\rm{1}}}{\rm{ + }}{{\rm{m}}_{\rm{2}}}{\rm{)}}{{{\rm{u'}}}^{\rm{2}}}}}{{\rm{L}}}\)
เมื่อ T คือความตึงเชือกถ้าต้องการ v0 ต่ำสุดที่ทำให้มวล m1, m2 วนครบรอบ ต้องให้ T = 0 ณ จุดสูงสุด (เชือกกำลังหย่อนพอดี)
จะได้
\(\begin{align*} {\rm{ (}}{{\rm{m}}_{\rm{1}}}{\rm{ + }}{{\rm{m}}_{\rm{2}}}\rm)g + T &= \dfrac{{{\rm{(}}{{\rm{m}}_{\rm{1}}}{\rm{ + }}{{\rm{m}}_{\rm{2}}}{\rm{)}}{{{\rm{u'}}}^{\rm{2}}}}}{{\rm{L}}}\\ {\rm{(}}{{\rm{m}}_{\rm{1}}}{\rm{ + }}{{\rm{m}}_{\rm{2}}}\rm)g + 0 &= \frac{{{\rm{(}}{{\rm{m}}_{\rm{1}}}{\rm{ + }}{{\rm{m}}_{\rm{2}}}{\rm{)}}{{{\rm{u'}}}^{\rm{2}}}}}{{\rm{L}}}\\ \rm g &= \frac{{{{{\rm{u'}}}^{\rm{2}}}}}{{\rm{L}}} \end{align*}\)
จาก (2)
\(\begin{align*} \rm gL &= {{\rm{u}}^{\rm{2}}} - 4{\rm{gL}}\\ \rm u &= \sqrt {{\rm{5gL}}} \end{align*}\)
จาก (1)
\(\begin{align*} \frac{{{{\rm{m}}_{\rm{1}}}}}{{{{\rm{m}}_{\rm{1}}}{\rm{ + }}{{\rm{m}}_{\rm{2}}}}}{{\rm{v}}_{\rm{0}}} &=\sqrt {{\rm{5gL}}} \\ {{\rm{v}}_{\rm{0}}}&=\left( {\frac{{{{\rm{m}}_{\rm{1}}}{\rm{ + }}{{\rm{m}}_{\rm{2}}}}}{{{{\rm{m}}_{\rm{1}}}}}} \right)\sqrt {{\rm{5gL}}} \end{align*}\)
| 23. | ถ้าดาวทรงกลมสม่ำเสมอสองดวง มีความหนาแน่นเท่ากัน แต่รัศมีไม่เท่ากัน แล้วปริมาณในข้อใดที่ดาวทั้งสองจะมีค่าเท่ากัน |
| A | ความเร็วหลุดพ้นที่ผิวของดาว |
| B | ความเร่งโน้มถ่วงที่ผิวของดาว |
| C | คาบในการโคจรของดาวเทียม เหนือผิวดาวพอดีในวงโคจรวงกลม |
| D | คาบในการโคจรของดาวเทียม ที่ระยะห่างใดๆ จากจุดศูนย์กลาง ในวงโคจรวงกลม |
| E | ไม่มีข้อใดถูก |
ตอบ (C)
ดาวสองดวงมี ρ เท่ากัน แต่ R1 ≠ R2 จะได้ว่า M1 ≠ M2 แต่
จาก กฎอนุรักษ์พลังงาน อนุภาคมวล m จะเคลื่อนที่ห่างจากดาว แล้วไปหยุดนิ่งพอดีที่ระยะอนันต์
B) ความเร่งที่ผิวของดาว (g) = \(\dfrac{{{\rm{GM}}}}{{{{\rm{R}}^{\rm{2}}}}}\) จะได้ g1 ≠ g2
C) คาบการโคจรดาวเทียม (T)
เขียนสมการเคลื่อนที่แบบวงกลม
ข้อ D) r ใดๆ โดยที่ r1 = r2 จะได้ว่า ดังนั้น T1 ≠ T2
ดังนั้น ตอบข้อ C)
ดาวสองดวงมี ρ เท่ากัน แต่ R1 ≠ R2 จะได้ว่า M1 ≠ M2 แต่
\(\begin{align*}
\frac{{{{\rm{M}}_{\rm{1}}}}}{{\frac{{\rm{4}}}{{\rm{3}}}{\rm{\pi R}}_{\rm{1}}^{\rm{3}}}} &= \frac{{{{\rm{M}}_{\rm{2}}}}}{{\frac{{\rm{4}}}{{\rm{3}}}{\rm{\pi R}}_{\rm{2}}^{\rm{3}}}} = {\rm{\rho }}\\
\frac{{{{\rm{M}}_{\rm{1}}}}}{{{\rm{R}}_{\rm{1}}^{\rm{3}}}} &= \frac{{{{\rm{M}}_{\rm{2}}}}}{{{\rm{R}}_{\rm{2}}^{\rm{3}}}}
\end{align*}\)
A) ให้ความเร็วหลุดพ้นที่ผิวดาว = vจาก กฎอนุรักษ์พลังงาน อนุภาคมวล m จะเคลื่อนที่ห่างจากดาว แล้วไปหยุดนิ่งพอดีที่ระยะอนันต์
\(\begin{align*}
\frac{1}{2}{\rm{m}}{{\rm{v}}^2} + \left( {\frac{{{\rm{ - G}}}}{{{\rm{MmR}}}}} \right) &= 0\\
\rm v &= \sqrt {\frac{{{\rm{2GM}}}}{{\rm{R}}}}
\end{align*}\)
จะได้ v1 ≠ v2B) ความเร่งที่ผิวของดาว (g) = \(\dfrac{{{\rm{GM}}}}{{{{\rm{R}}^{\rm{2}}}}}\) จะได้ g1 ≠ g2
C) คาบการโคจรดาวเทียม (T)
เขียนสมการเคลื่อนที่แบบวงกลม
\(\begin{align*}
{\rm{m}}{{\rm{\omega }}^{\rm{2}}}\rm r &= \frac{{{\rm{GMm}}}}{{{{\rm{r}}^{\rm{2}}}}}\\
\omega &= \sqrt {\frac{{{\rm{GM}}}}{{{{\rm{r}}^{\rm{3}}}}}}
\end{align*}\)
หรือ
\(\rm T = \dfrac{{{\rm{2\pi }}}}{{\rm{\omega }}}{\rm{ = 2\pi }}\sqrt {\dfrac{{\rm{1}}}{{\rm{G}}}\dfrac{{{{\rm{r}}^{\rm{3}}}}}{{\rm{M}}}}\)
ข้อ C) r = R ใดๆ จะได้ว่า \({\rm{T }} \propto \sqrt {\dfrac{{{{\rm{R}}^{\rm{3}}}}}{{\rm{M}}}} \) ดังนั้น T1 = T2ข้อ D) r ใดๆ โดยที่ r1 = r2 จะได้ว่า ดังนั้น T1 ≠ T2
ดังนั้น ตอบข้อ C)
| 24. | ยิงบอลขึ้นฟ้าจากพื้นด้วยอัตราเร็วต้นในแนวตั้ง v0 และบอลที่ตกกลับลงมาจะกระเด้งกับพื้นในแนวตั้ง เนื่องจากการชนนั้นไม่ยืดหยุ่น บอลจึงสูญเสียความเร็วไปตามสัดส่วนค่าหนึ่งทุกครั้งที่เกิดการกระเด้ง เช่น ถ้าอัตราเร็วก่อนกระทบพื้นคือ v แล้วอัตราเร็วหลังกระทบพื้นจะเท่ากับ rv โดยค่าคงที่ r < 1 แล้วเวลารวมที่บอลเคลื่อนที่ไปได้จะเท่ากับข้อใด สมมุติว่าเวลาที่บอลกระทบพื้นสั้นมาก |
| A | \(\rm \dfrac{2 v_0}{g} \dfrac{1}{1-r}\) |
| B | \(\rm \dfrac{v_0}{g} \dfrac{r}{1-r}\) |
| C | \(\rm \dfrac{2v_0}{g} \dfrac{1-r}{r}\) |
| D | \(\rm \dfrac{2v_0}{g} \dfrac{1}{1-r^2}\) |
| E | \(\rm \dfrac{2v_0}{g} \dfrac{1}{1+(1-r)^2}\) |
ตอบ (A)
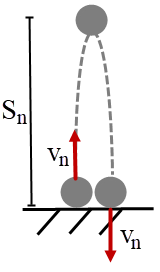 พิจารณาการตกกระทบพื้นครั้งที่ ใดๆ
พิจารณาการตกกระทบพื้นครั้งที่ ใดๆ
จะได้ vn = rnv0

จะได้ vn = rnv0
tn (เวลาเด้งขึ้น – ลง) = \(2\left( {\dfrac{{{{\rm{v}}_{\rm{n}}}}}{{\rm{g}}}} \right)\)
tn = \(\dfrac{{2{{\rm{v}}_{\rm{0}}}}}{{\rm{g}}}{{\rm{r}}^{\rm{n}}}\)
ดังนั้น tรวม = \(\displaystyle\sum\limits_{{\rm{n = 0}}}^\infty {{{\rm{t}}_{\rm{n}}}} {\rm{ = }}\frac{{{\rm{2}}{{\rm{v}}_{\rm{0}}}}}{{\rm{g}}}\left( {{\rm{1 + r + }}{{\rm{r}}^{\rm{2}}}{\rm{ + }}...} \right){\rm{ = }}\frac{{{\rm{2}}{{\rm{v}}_{\rm{0}}}}}{{\rm{g}}}\left( {\frac{1}{{1 - {\rm{r}}}}} \right)\)| 25. | ดาวเทียมสองดวงถูกยิงออกจากตำแหน่ง R จากศูนย์กลางดาวเคราะห์ที่มีรัศมีเล็กมาก และดาวเทียมทั้งสองถูกยิงออกไปในทิศตั้งฉากกับเส้นรัศมี ถ้าดาวเทียมดวงแรกถูกยิงด้วยอัตราเร็ว v0 และเข้าสู่วงโคจรวงกลม ส่วนดาวเทียมดวงที่สองถูกยิงด้วยอัตราเร็ว \(\dfrac{1}{2}\)v0 แล้วระยะใกล้สุดของดาวเทียมที่สองกับดาวเคราะห์ขณะอยู่ในวงโคจรเท่ากับข้อใด |
| A | \(\rm\dfrac{1}{\sqrt2}R\) |
| B | \(\rm\dfrac{1}{2}R\) |
| C | \(\rm\dfrac{1}{3}R\) |
| D | \(\rm\dfrac{1}{4}R\) |
| E | \(\rm\dfrac{1}{7}R\) |
ตอบ (E)
ให้ดาวเคราะห์มวล = M
พิจารณาดาวเทียมดวงแรก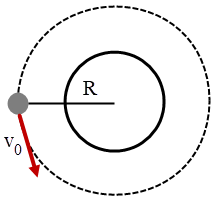 สมการการเคลื่อนที่วงกลม
สมการการเคลื่อนที่วงกลม
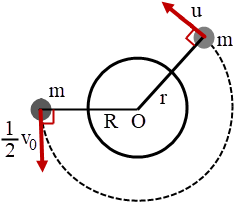 ที่ระยะใกล้กับดาวที่สุด ดาวเทียมจะมีความเร็ว u และตั้งฉากกับเส้นรัศมี ระยะจาก O ถึงมวล เท่ากับ r
ที่ระยะใกล้กับดาวที่สุด ดาวเทียมจะมีความเร็ว u และตั้งฉากกับเส้นรัศมี ระยะจาก O ถึงมวล เท่ากับ r
จากกฎอนุรักษ์พลังงาน
จากกฎอนุรักษ์โมเมนตัมเชิงมุม
ดังนั้น ระยะที่ใกล้ดาวเคราะที่สุด คือ \(\rm \dfrac{R}{7}\)
ให้ดาวเคราะห์มวล = M
พิจารณาดาวเทียมดวงแรก

\(\begin{align*} \frac{{{\rm{mv}}_{\rm{0}}^{\rm{2}}}}{{\rm{R}}} &= \frac{{{\rm{GMm}}}}{{{{\rm{R}}^{\rm{2}}}}}\\ {\rm{v}}_{\rm{0}}^{\rm{2}} &= \frac{{{\rm{GM}}}}{{\rm{R}}} \end{align*}\)
พิจารณาดาวเทียมดวงที่สอง

จากกฎอนุรักษ์พลังงาน
\(\begin{align*} \frac{{\rm{1}}}{{\rm{2}}}{\rm{m}}{{\rm{u}}^{\rm{2}}} - \frac{{{\rm{GMm}}}}{{\rm{r}}} &= \frac{{\rm{1}}}{{\rm{2}}}{\rm{m}}{\left( {\frac{{\rm{1}}}{{\rm{2}}}{{\rm{v}}_{\rm{0}}}} \right)^{\rm{2}}} - \frac{{{\rm{GMm}}}}{{\rm{R}}}\\ \frac{{\rm{1}}}{{\rm{2}}}{{\rm{u}}^{\rm{2}}} - \frac{{{\rm{GM}}}}{{\rm{r}}} &= \frac{{\rm{1}}}{{\rm{8}}}{\rm{v}}_0^2 - \frac{{{\rm{GM}}}}{{\rm{R}}} \end{align*}\)
จาก \({\rm{v}}_{\rm{0}}^{\rm{2}} = \dfrac{{{\rm{GM}}}}{{\rm{R}}}\)
\(\dfrac{{\rm{1}}}{{\rm{2}}}{{\rm{u}}^{\rm{2}}} - \dfrac{{{\rm{GM}}}}{{\rm{r}}} = \dfrac{{\rm{1}}}{{\rm{8}}}\dfrac{{{\rm{GM}}}}{{\rm{R}}} - \dfrac{{{\rm{GM}}}}{{\rm{R}}}\)
\(\dfrac{{\rm{1}}}{{\rm{2}}}{{\rm{u}}^{\rm{2}}} - \dfrac{{{\rm{GM}}}}{{\rm{r}}} = - \dfrac{7}{{\rm{8}}}\dfrac{{{\rm{GM}}}}{{\rm{R}}}\) --- (1)
จากกฎอนุรักษ์โมเมนตัมเชิงมุม
\({\rm{mR}}\left( {\dfrac{{\rm{1}}}{{\rm{2}}}} \right){{\rm{v}}_{\rm{0}}}{\rm{ = mru}}\)
\({\rm{u = }}\left( {\dfrac{{\rm{1}}}{{\rm{2}}}{{\rm{v}}_{\rm{0}}}} \right)\left( {\dfrac{{\rm{R}}}{{\rm{r}}}} \right)\) --- (2)
แทน (2) และ \({\rm{v}}_{\rm{0}}^{\rm{2}} = \dfrac{{{\rm{GM}}}}{{\rm{R}}}\) ใน (1)
\(\begin{align*} \frac{{\rm{1}}}{{\rm{2}}}{\left( {\frac{{\rm{1}}}{{\rm{2}}}{{\rm{v}}_{\rm{0}}}} \right)^{\rm{2}}}\left( {\frac{{{{\rm{R}}^{\rm{2}}}}}{{{{\rm{r}}^{\rm{2}}}}}} \right) - \frac{{{\rm{GM}}}}{{\rm{r}}} &= - \frac{7}{{\rm{8}}}\frac{{{\rm{GM}}}}{{\rm{R}}}\\ \frac{{\rm{1}}}{{\rm{8}}}\left( {\frac{{{\rm{GM}}}}{{\rm{R}}}} \right)\left( {\frac{{{{\rm{R}}^{\rm{2}}}}}{{{{\rm{r}}^{\rm{2}}}}}} \right) - \frac{{{\rm{GM}}}}{{\rm{r}}} &= - \frac{7}{{\rm{8}}}\frac{{{\rm{GM}}}}{{\rm{R}}}\\ \frac{{\rm{1}}}{{\rm{8}}}\left( {\frac{{\rm{R}}}{{{{\rm{r}}^{\rm{2}}}}}} \right) - \frac{{\rm{1}}}{{\rm{r}}} &= - \frac{7}{{\rm{8}}}\frac{{\rm{1}}}{{\rm{R}}} \end{align*}\)
คูณ 8Rr2
\(\begin{align*} \rm {R^2} - 8Rr &= \rm - 7{r^2}\\ \rm 7{r^2} - 8Rr\, + {R^2} &= 0\\ \rm (7r - R)(r - R) &= 0\\ \rm r &= \rm R,\frac{R}{7} \end{align*}\)
เนื่องจาก R เป็นระยะขณะเริ่มปล่อย จึงไม่ใช่คำตอบดังนั้น ระยะที่ใกล้ดาวเคราะที่สุด คือ \(\rm \dfrac{R}{7}\)

